A Heuristic polynomial gcd algorithm

This is an example of the general scheme of heuristics. In this case we use a many-to-one mapping from polynomial variables onto the integers. This is an evaluation mapping. Under certain conditions satisfied by the size of the coefficients in the result and the evaluation value, we can invert this mapping.

We will assume the following:

• Computing multivariate polynomial gcds is difficult.
• Computing integer gcds is easy (even if the integers are thousands of digits long).
• Exact polynomial division is easy.

Let a(x) and b(x) be the polynomials. We can assume without loss of generality that these polynomials are over the integers and primitive (the content, that is the integer gcd of the coefficients, has been divided out). Each polynomial can be decomposed in two parts: the gcd and its cofactor.

$$g(x) = \gcd ( a(x), b(x) )$$

a(x) = g(x) c_a(x)

b(x) = g(x) c_b(x)

where c_a(x) and c_b(x) are relatively prime polynomials. We now choose our evaluation point n to be an integer sufficiently large (as will be defined later) and compute a(n) and b(n). Let

$${\rm igcd}( a(n), b(n) ) = g(n) r(n)$$

where r(n) is an unknown integer computed as the integer gcd of c_a(n) and c_b(n). For our purposes r(n) is a spurious factor. If it becomes too large in magnitude, it may prevent correct lifting of the answer.

We may have two problems:

• from g(n) we may not reconstruct g(x)
• from r(n) g(n) we may not reconstruct r(n) g(x)

Let g^*(x) be the polynomial reconstructed from r(n) g(n). This reconstruction is done from the lowest degree coefficient to the highest by symmetric mod n operations. The loop for this reconstruction is as follows:

    # Algorithm to lift a polynomial from an integer
    #  i.e. reverse the evaluation of g(x) at x=n

    g := igcd( a(n), b(n) );
    gstar := 0;
    for i from 0 while g <> 0 do
        c := mods(g,n);
        gstar := gstar + c*x^i;
        g := (g-c)/n
        od;

In Maple this lifting operation is supported by the kernel and called genpoly. The above code would look like

    gstar := genpoly( igcd( a(n), b(n) ), n, x );

It is obvious from the lifting, that all the coefficients lifted are $\vert c_i\vert \le n/2$. So, if n is chosen to be at least twice as large as the largest coefficient in g(x)r(n), then the lifting will always be successful.

But this has two problems. First we can only estimate the coefficients of g(x) and have no idea of the magnitude of r(n). Secondly, we would like to choose n to be as small as possible, so that the integer gcd computations are efficient. This second argument becomes very important for the multivariate case when we have to recursively evaluate for each variable; then the successive n_i will become doubly exponentially large.

So instead of guaranteeing that we choose a safe (large enough) n, we will choose a minimal one and test to make sure that the results are correct. The verification will be done as follows:

Once that we have obtained g^*(x) we perform two trial divisions: we test whether g^*(x) divides a(x) and whether it divides b(x). If this test fails, then the lifting was incorrect due to one of the above reasons. If this test passes, then g^*(x) is an integer multiple of g(x), i.e. r(n) g(x)and by removing its content we obtain g(x).

    # algorithm GCDHEU

    n := initial_n;
    while true do
        gstar := genpoly( igcd( a(n), b(n) ), n, x );
        if divide(a(x),gstar) and
           divide(b(x),gstar) then break
        else n := 2*n+1 fi
        od;
    g := gstar / icontent(gstar);

Proof that the primitive part of g^*(x) is the correct gcd.

By passing the two division tests, we know that g^*(x) is a factor of the gcd (it divides both polynomials). We will now prove that the degree of g^*(x) is not less than the degree of g(x) and hence it must be equal.

So we must find a large enough n such that g(n) will lift a polynomial with the correct degree (or larger). Let

$$g(x) = g_n ( x-\alpha_1) (x-\alpha_2) ...$$

and

$$r(n) g(n) = r(n) g_n (n-\alpha_1) (n-\alpha_2) ...$$

To guarantee that g^*(x) will have the correct degree, this value should be larger than $\frac{n^{d_g}}{2}$where d_g is the degree of g(x), or

$$r(n) g_n (1-\alpha_1/n) (1-\alpha_2/n) ... > 1/2$$

Assuming the worst case, i.e. r(n)=1, g_n=1 and letting $\alpha = \max_i \vert\alpha_i\vert$ we obtain

$$(1 - \alpha/n) ^ {d_g} > 1/2$$

or

$$n > \frac {\alpha} {1-2^{-1/d_g}} > \frac {d_g \alpha} {\log 2}$$

For such n, the algorithm GCDHEU produces the correct gcd of a(x) and b(x). Notice that this is a heuristic because the loop may never terminate, but if it terminates, the result is correct. This type of heuristic is commonly called ``Las Vegas''.

The roots of g(x) are not known, but these should be roots of both a(x) and b(x). Then if n satisfies

$$n > \frac { \min( deg(a(x)), deg(b(x)) ) \min ( \max_{a(\alph... ..._i\vert, \max_{b(\alpha_i)=0} \vert \alpha_i\vert )} { \log 2}$$

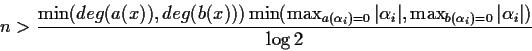
How large is r(n)?

It is easy to see that there are polynomials which for which every evaluation over an integer give values which are divisible by d!This is called the fixed divisor of a polynomial. E.g.

p(x) = x(x-1)(x-2)(x-3) ... (x-d+1)

is always divisible by d!. In particular, p(x) and p(x+d) are relatively prime polynomials and ${\rm igcd}( p(n), p(n+d) ) = d!$ for every value of n. So r(n) could be rather large (in these cases it is composed of small prime factors).

It is useful to bound r(n). The fixed divisors can be bounded using the original polynomials a(x) and b(x). As a matter of fact it is very easy to compute the fixed divisors:

    # Compute the fixed divisor of a(x)
    fd := a(0);
    for i while fd > i! do fd := igcd( fd, a(i) ) od;

or to compute the common fixed divisor of both a(x) and b(x) (a multiple of r(n)).

    # Compute the fixed divisor of g(x)
    fd := igcd( a(0), b(0) );
    for i while fd > i! do fd := igcd( fd, a(i), b(i) ) od;

Other common factors may arise with high probability. For example the polynomial p(x) = x(x-1)(x-3)(x-4)+5does not have a fixed divisor. p(x), p(x+10) are relatively prime, yet for random integers 80% of the time their r(n) is a multiple of 5.