Further improvements

Once that we have computed the minimum value of n and the first value of r(n) g(n), it is possible to bound the degree of g(x).

From the equation bounding r(n)g(n) we can derive

$$g(n) = g_n (n-\alpha_1) ... > g_n (n-\alpha)^{d_g} > \frac {g_n n^{d_g}} {2}$$

or

$$d_g < \log_n \frac{2g(n)}{g_n} \le \log_n 2r(n)g(n)$$

This bound is rather tight. The first use of this bound is to estimate n itself, in case that the first iteration did not lift a correct gcd.

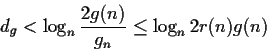
The second use of the upper bound on d_g is more interesting. So far we have tried to lift g(x). But it is equally possible to lift one of the cofactors, that is c_a(x) or c_b(x). By knowing the degrees of a(x), b(x) and an estimate of the degree of g(x) we can decide to lift the polynomial with the lowest degree (which in practice will the least expensive to lift).

    # Cofactor lifting

    n := any_choice;
    an := a(n);
    ca := genpoly( an / igcd( an, b(n) ), n, x );
    if divide( a(x), ca, 'g' ) and
        divide( b, g ) then # success
    else g := FAIL fi;

The cofactor lifting has a significant advantage on the previous lifting. The above procedure, if successful, produces the correct result for any value of n. So we can choose n as small as we wish. The proof of correctness is based on the fact that a poor choice of n or r(n) may lift a c_a(x) of lower degree, which means that g(x) will be of higher degree. Hence this will never pass the test.

If r(n) is not 1, then the above procedure will not work, i.e. it will always fail. This can be improved by finding the common fixed divisor of both polynomials as shown above. It is also possible to allow for some extra spurious factors in r(n) and multiply a(n) by small integers.

The combination of lifting the gcd or one of its cofactors is quite complementary. It happens for unbalanced problems that either the gcd is large (large degree and large coefficients) or the cofactor is large. The lifting of non-large polynomials is more efficient (will not need to increase n).

The main paper on this subject is [1]. The original proofs and the actual algorithm implemented in Maple differ from the one presented here.