


Next: Non-standard uses of signatures
Up: Modular mappings
Previous: Primes suitable for nested
Computing signatures of logarithms is more complicated in the sense that
we do not know how to compute them in time polynomial in the size of the
problem.
The signatures will be computed as
where n and m = kn+1 are primes,
E=Sm(e)=pk is the base of the
exponential function and p is a primitive root (mod m).
The 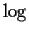 is the discrete logarithm, sometimes called the index function.
It is defined by
is the discrete logarithm, sometimes called the index function.
It is defined by
Notice the different ground fields on which we are computing here.
This is similar to the 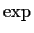 function, where the exponent arithmetic
was done on a different field, but in reverse.
function, where the exponent arithmetic
was done on a different field, but in reverse.
If the signature of the argument is 0, we cannot compute the
discrete logarithm.
This is a case analogous to a division by zero, and we will proceed
as with it.
I.e. we will recursively test whether the argument is 0.
If it is, then the computation does not make sense and it is aborted.
If it is not, then we have found an n for which the signature is
non-zero, and we continue the computation in this field.
With such a value for E, not being a primitive root, there will
be discrete logarithms that will not be possible to compute.
This problem is tricky to solve, but we can use the fact that
the range of the discrete logarithm is normally 0 ... m-2,
and we fold this range to 0 ... n-1.
Let r=pn, then r is a kth root of unity, and 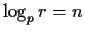 .
Multiplying the arguments of the logarithms by any power of rwill not change their signature.
If the base of the logarithms is p, then it is clear that
.
Multiplying the arguments of the logarithms by any power of rwill not change their signature.
If the base of the logarithms is p, then it is clear that
In other words, the signatures of logarithms group values of the
arguments in equivalence classes of size k.
The generator of these classes of equivalence is r.
When we compute discrete logarithms base E, then this class
of equivalence will have one member having a logarithm, and all the
others being not representable.
We will use as a signature of any argument, the signature of
any of the members of its equivalence class.
It turns out that this is equivalent to computing the discrete
logarithms as:
A numerical example helps to understands all these computations and
problems.
Assume that n=13 and m=53 and hence k=4.
Let p=2 which is a primitive root (mod 53).
Then
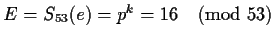 and
and
 .
We would like to prove that
.
We would like to prove that
The signatures of the arguments are
 and Sm(8)=8.
Now,
and Sm(8)=8.
Now,
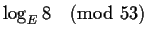 does not exist.
I.e. there is no value c such that
does not exist.
I.e. there is no value c such that
 .
But 8 is in a class of equivalence
.
But 8 is in a class of equivalence
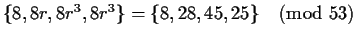 .
Of the four components of this equivalence class, only 28 has
a discrete logarithm base E,
.
Of the four components of this equivalence class, only 28 has
a discrete logarithm base E,
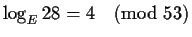 .
Similarly for 23,
.
Similarly for 23,
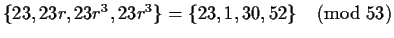 , and only 1
has a logarithm,
, and only 1
has a logarithm, 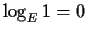 .
Notice that
.
Notice that
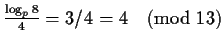 and
and
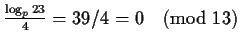 .
This gives
.
This gives
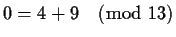 which verifies the initial equation.
which verifies the initial equation.



Next: Non-standard uses of signatures
Up: Modular mappings
Previous: Primes suitable for nested
Gaston Gonnet
1999-07-04
![]() .
Multiplying the arguments of the logarithms by any power of rwill not change their signature.
If the base of the logarithms is p, then it is clear that
.
Multiplying the arguments of the logarithms by any power of rwill not change their signature.
If the base of the logarithms is p, then it is clear that
![]() and
and
![]() .
We would like to prove that
.
We would like to prove that