Non-standard uses of signatures for general problems

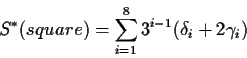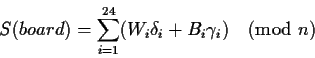
The game of Mühle (9 Men Morris) is a common game in Europe. It is played on a square board consisting of three concentric squares. Black and white pebbles (or men) are placed on the crossings and later moved around. The following is a picture of the board with the playing positions numbered from 1 to 24.

            1--------------------2--------------------3
            |                    |                    |
            |                    |                    |
            |      9-------------10------------11     |
            |      |             |              |     |
            |      |             |              |     |
            |      |    17------18-------19     |     |
            |      |    |                 |     |     |
            |      |    |                 |     |     |
            8-----16----24               20----12-----4
            |      |    |                 |     |     |
            |      |    |                 |     |     |
            |      |    23------22-------21     |     |
            |      |             |              |     |
            |      |             |              |     |
            |     15------------14-------------13     |
            |                    |                    |
            |                    |                    |
            7--------------------6--------------------5

For the purposes of building a table of boards and searching particular configurations in this table, it is extremely appealing to have a signature for each instance of the board. By a particular instance we mean several black and white pebbles in various positions.

Notice that the board instances, for the purposes of strategy, validity, moves, etc. form classes of equivalence. Each class has a maximum of 32 different boards and these are generated by:

4 rotations
• 2 axial symmetries
• 2 inner-outer square swaps
• 2 colour swaps

(Whether it is a white move or a black move is not part of the board, and hence it should be handled separately.)

Because of the large number of possible boards, it is assumed that that each equivalence class of boards will be stored only once. This will have an extra cost that will be paid at searching and/or insertion time. For this there are two alternatives

(1) Insert any of the boards at insertion time. At searching time we will have to search all of the members of the equivalence class, that is up to 32 searches.

(2) Insert a canonical one (it is quite easy to select a canonical one when we use signatures, we can select the one with the smallest signature). At searching time we search only once after having selected the signature of the canonical one.

The second policy is superior as we do only one search in the database. Notice that following a successful signature search we still have to compare the boards. Different boards may have equal signatures. This comparison will seldom fail, it will almost always return true. I.e. signature collisions are rare, they occur with probability O(1/n).

Additive signature functions for Mühle.

Let the positions in the board be numbered from 1 to 24 as shown above. Let W_i and B_i be random numbers chosen uniformly from [0,n-1] unless otherwise stated. A linear signature is defined by

$$S( board ) = \sum_{i=1}^{24} ( W_i \delta_i + B_i \gamma_i ) \pmod{n}$$

where $\delta_i=1$ when there is a white pebble in position i and it is 0 otherwise and similarly $\gamma_i=1$ for the black. The main operation in a linear signature is multiplication by a factor, i.e. $\alpha S$, which is equivalent to multiplying each B_i and W_iby $\alpha$. If the number of men, k, is known, a linear transformation of the form $\alpha S + k\beta$, will map every B_i to $\alpha B_i+\beta$, and similarly for W_i.

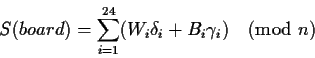
Rotations of the board.

To do rotations by multiplication the following equations must hold:

$$\alpha B_1 = B_3,\;\;\;\alpha B_3 = B_5,\;\;\;\alpha B_5 = B_7, \;\;\;\alpha B_7 = B_1$$

etc. This means that $\alpha^4-1=(\alpha+1)(\alpha-1)(\alpha^2+1) = 0 \pmod{n}$. We can choose $\alpha$ to be a non-trivial root of the above, for example for $n=123457,\;\alpha=7738$, and if we compute all the W_i from W₁, W₂, W₉, W₁₀, W₁₇, W₁₈ and similarly for B_iwe can rotate the board 90 degrees by multiplication by $\alpha$. This has a flaw which is difficult to cure, as even for the non-trivial $\alpha$, $\alpha^2=-1$. This means that diametrically opposed men of the same colour will cancel out. This cancellation is bad as it happens for any possible value of nand confuses a board with no men in two corners with a similar board with two equally coloured men in these corners. Other cancellations are also possible. Consequently we will not use this technique to compute rotations.

Colour swaps.

If we select $W_i = -B_i \pmod{n}$, colour swap is achieved by complementing the signature. Cancellations cannot happen as we cannot have two men in a single position. It we have no other conditions on the W_i and B_i this is a good solution.

Inner-outer square swaps.

This is not possible to achieve by simple multiplication, as

$$\alpha B_1 = B_{17},\;\;\; \alpha B_{17}=B_1, \;\;\; \alpha B_9 = B_9$$

has only one non-interesting solution. A relatively general technique may be used to solve this problem. If we define a new signature over a single square as

$$S^*(board) = \sum_{i=1}^8 (W_i \delta_i + B_i \gamma_i) \pmod{n}$$

then the signature of the entire board can be represented by a triplet

S(board) = (S^*(outer), S^*(middle), S^*(inner))

The inner-outer swap of the signature (a,b,c) is (c,b,a). If this is combined with the colour swap as described above, then the four combinations of colour swap and inner-outer swaps are

$$(a,b,c),\;\;\; (c,b,a),\;\;\; (-a,-b,-c),\;\;\; (-c,-b,-a)$$

Since we are interested in the minimum signature (in the case of a tuple of values, the ordering will be a lexicographical ordering of the elements left to right), we first choose the minimum between a,-a,c,-c and only in cases of multiple minima we need to compare further.

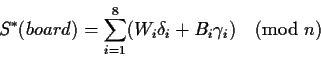
Axial symmetries.

There is again no obvious solution for symmetries, as a vertical axis symmetry would have to satisfy:

$$\alpha W_1 = W_3,\;\;\; \alpha W_3 = W_1,\;\;\; \alpha W_2 = W_2$$

which gives non-interesting solutions.

Question / exercise.

What are the advantages and disadvantages of the signature defined by the tuple:

S(board) = ( S^*(outer) S^*(middle), S^*(inner) S^*(middle) )

As a final remark, it should be noticed that in reducing the signatures of the entire board to 3 signatures over squares, the cardinality of each individual S^* is only 3⁸=6561. So at this point it is probably more useful to use an exact mapping between squares and integers, for example

$$S^*(square) = \sum_{i=1}^8 3^{i-1}(\delta_i+2\gamma_i)$$

Rotations by 90 degrees and symmetries can now be precomputed and stored in tables, their size will be reasonable for any computer. Then all the computation of signatures is reduced to table lookups and the operations done for colour and inner-outer swaps. The resulting signatures will also be unique, so this will save the comparison for equal boards once that the signatures match. This is interesting because with the ideas of signatures we have gone back to a better deterministic algorithm.