Next: Signature of a derivative
Up: Open problems with signatures
Previous: Signature of
The signature of 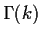 or at least the signature of k!are very expensive, O(k) operations, to compute.
This is not good, as for an unknown x,
or at least the signature of k!are very expensive, O(k) operations, to compute.
This is not good, as for an unknown x, 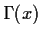 would
require the computation of Sn(x)! which is O(n).
This question in itself is very interesting.
Is it possible to compute
would
require the computation of Sn(x)! which is O(n).
This question in itself is very interesting.
Is it possible to compute
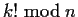 in time less than O(k)?
This question is open, and very doubtful.
If it would be possible, we could do integer factorization in
the same time.
Non-trivial factors of n can be computed from by
in time less than O(k)?
This question is open, and very doubtful.
If it would be possible, we could do integer factorization in
the same time.
Non-trivial factors of n can be computed from by
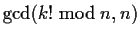 .
Is it possible to fake the signature of
.
Is it possible to fake the signature of 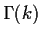 ?
The only relations between
?
The only relations between 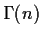 and
and 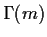 are
when n-m is an integer and the expression is of size O(|n-m|).
Additional care has to be taken with the half argument relations,
are
when n-m is an integer and the expression is of size O(|n-m|).
Additional care has to be taken with the half argument relations,
its extensions and with the reflection formula.



Next: Signature of a derivative
Up: Open problems with signatures
Previous: Signature of
Gaston Gonnet
1999-07-04