Signature of a derivative

A partially resolved problem is the computation of the signature of the derivative of an expression with respect to a given variable, say x. This can be done by recursing on the original expression, but it is not possible to do (or at least not known to us) just from the signatures. The rules for computing the signature of a derivative are straightforward, i.e.

S_n( D_x(ab) ) = S_n( D_x(a) ) S_n(b) + S_n(a) S_n( D_x(b) )

$$S_n( D_x( \mbox{constant} )) = 0$$

S_n( D_x( x ) ) = 1

etc. In general we want to compute signatures from signatures, and not recursively on the original expression. Just from the complexity point of view, if intermediate results are not stored, the above computation would be exponential in the number of nested products. This is clearly undesirable. In other words, an optimal signature is one which can be computed as

S_n( g(a,b, ... )) = g^*( S_n(a), S_n(b), ... )

This does not appear to be possible for the derivative. Computing the signature of an indefinite integral does not make sense as there is an arbitrary integration constant which makes any result possible. Notice that the integration constant may be hidden in the expression, and hence impossible to isolate. For example

$$\int \frac{1}{x} dx = \ln 2x$$

is a correct indefinite integral with a hidden integration constant. Although this is still partly open, it is possible to verify that a given expression is the integral of another. All what has been said about integration and differentiation can be mapped one-to-one to summations and the 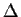$\Delta$ difference operator.