


Next: Suitable point for expansion
Up: Various methods for algebraic
Previous: Various methods for algebraic
This method expands the expression
F(x,y, ... a,b,...) - G(x,y, ... m,n,... )
as a multivariate series in x, y, ... (all the main variables).
If a match exists, all the coefficients must be equal to zero.
So the matching problem is reduced to solving a system of
equations in the parameter variables.
Notice that each coefficient of the multivariate series will
not contain any occurrence of the main variables, hence the
coefficients are expressions in the parameters and the
pattern variables.
A solution of equating several coefficients to 0 in terms of
the pattern variables should be substituted and checked in
the original pattern.
If at any point, a coefficient cannot be equated to zero, then
there is no solution (provable) to the matching problem.
For example, to solve the matching of
we expand
 around x=0 and obtain
around x=0 and obtain
The coefficient of the series must be equal to zero, this means
From the first equation we conclude that
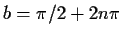 for any
integer n.
This value of b satisfies the second equation.
The third equation becomes a2-1=0 which has two solutions
for any
integer n.
This value of b satisfies the second equation.
The third equation becomes a2-1=0 which has two solutions
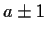 .
Plugging in any of these solutions in the original pattern,
and simplifying, we arrive at
.
Plugging in any of these solutions in the original pattern,
and simplifying, we arrive at 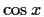 and hence they are
a solution of our matching problem.
and hence they are
a solution of our matching problem.
This heuristic is very powerful, but it has several pitfalls.
Some of them are avoidable.



Next: Suitable point for expansion
Up: Various methods for algebraic
Previous: Various methods for algebraic
Gaston Gonnet
1999-07-04