


Next: How many terms to
Up: Series method
Previous: Series method
In the above example we expanded the series around 0, and it
worked.
Expanding around any arbitrary point should also work, but
the complexity of the resulting equations may be too high to
produce a solution.
In other cases, the series may not be possible to expand at
the given point.
For example
cannot be expanded around x=0 because the pattern part
has its leading coefficient powered to r+p, which is unknown.
In such cases, most systems fail to expand, and the algorithm
mentioned above will not work.
Expanding around 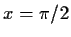 does not work either, as
does not work either, as 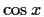 will have an unknown exponent in its leading term.
Expanding around x=1 (or around any other non-special value)
gives a system of equations which is virtually impossible to
solve.
will have an unknown exponent in its leading term.
Expanding around x=1 (or around any other non-special value)
gives a system of equations which is virtually impossible to
solve.
The matching
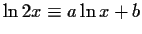 , will fail if expanded
at x=0 because there is no series in x (the series is in
, will fail if expanded
at x=0 because there is no series in x (the series is in
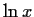 ).
In this case, expanding around x=1 works well
).
In this case, expanding around x=1 works well
giving the solution 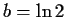 , a=1 from the first two coefficients.
, a=1 from the first two coefficients.
For simplicity, in particular for simplicity of the resulting
system of equations, it is best to expand at simple
values.
If these do not work, expanding at a random rational should work.
The main drawback of using random points of expansion is that
the corresponding system of equations may be too complicated to solve.



Next: How many terms to
Up: Series method
Previous: Series method
Gaston Gonnet
1999-07-04
![]() , will fail if expanded
at x=0 because there is no series in x (the series is in
, will fail if expanded
at x=0 because there is no series in x (the series is in
![]() ).
In this case, expanding around x=1 works well
).
In this case, expanding around x=1 works well