


Next: Finding simple relations among
Up: Modular mappings
Previous: Field/congruence enlargement
Signatures of unknowns should be random, and should not satisfy
any simple relation between each other.
We must beware of random number generators, which may give results
which are mathematically related.
Choosing the signatures of the ith unknown as
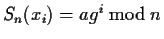 is not very good, the expression
x0x3/(x1x2)-1 will have
signature 0 for any value of a, g and n.
is not very good, the expression
x0x3/(x1x2)-1 will have
signature 0 for any value of a, g and n.
Polynomials are also very poor generators of signatures.
For example, suppose that we use a polynomial p(x) to
generate the signatures of unknowns, by using
Sn(xi) = p(i).
It happens that
p(x+1)+p(x+2)+p(x+6) = p(x)+p(x+4)+p(x+5)
for any polynomial of degree 2.
So
Sn( x1+x2+x6 - (x0+x4+x5) ) = 0for any arbitrary quadratic polynomial and any value of n.
This is highly undesirable.
A good generator for this purpose is algorithm A (Additive
number generator) described in Knuth, The Art of Computer Programming,
vol 2, second edition, page 27.
Another good method is to use a double-mod random number generator,
i.e.
where 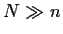 and (N,n)=1.
and (N,n)=1.
Gaston Gonnet
1999-07-04