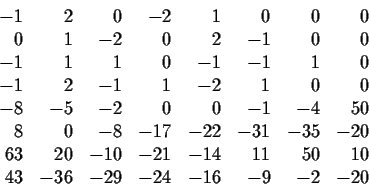Next: Rational numbers
Up: Signature of unknowns
Previous: Signature of unknowns
The above relationship,
p(x+1)+p(x+2)+p(x+6) = p(x)+p(x+4)+p(x+5)
is a relation that will hold for any polynomial of degree 2.
It is interesting as a side topic to be able to generate this
kind of simple relationships, not just for coefficients 1 and -1,
but for small coefficients.
This can be resolved with signatures of expressions and the
LLL lattice reduction algorithm, and it is a very good example
of both.
The problem can be formalized as follows:
we are looking for a polynomial
p(x) = adxd+...a1x+a0such that
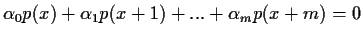 for any coefficients in p(x) and for any value of x.
Furthermore, we are interested in the case where the
for any coefficients in p(x) and for any value of x.
Furthermore, we are interested in the case where the 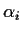 coefficients are small.
coefficients are small.
For this we will construct the
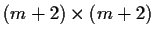 matrix
matrix
where b is an integer blow up factor, used to make sure
that for the shortest vectors, a 0 will be in that column, and
hence the corresponding relations with the polynomials are exact.
The last column contains all the signatures of the unknown polynomial,
which are computed (mod n).
The last row serves the purpose of computing the linear combinations
of the signatures (mod n).
For example, if we let d=2,
n=100000007, m=6 and b=10 and
the random variables assigned to the unknowns:
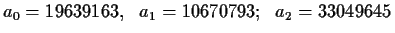 and
x=56110369 then the matrix is
and
x=56110369 then the matrix is
Applying the LLL algorithm to the above produces the reduced matrix:
From these short vectors we can conclude the previous relation
from row 3 and the relation
2p(x+1)+p(x+4) = p(x)+2p(x+3)
from row 1.
These relations can be verified with a computer algebra system if
necessary.



Next: Rational numbers
Up: Signature of unknowns
Previous: Signature of unknowns
Gaston Gonnet
1999-07-04
![]() matrix
matrix
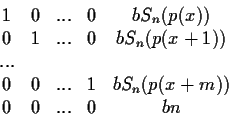
![]() and
x=56110369 then the matrix is
and
x=56110369 then the matrix is