


Next: Examples
Up: Idea of the algorithm
Previous: Idea of the algorithm
Figure:
Algorithm 4.0
 |
Given is a set of sequences
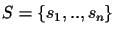 .
First, the optimal circular order C is
calculated with a TSP algorithm. The sequences are renamed with
respect to that order. Starting with the optimal circular order
C, each of the n-1 pairs of neighboring leaves are swapped
(see Algorithm 4.1.1) and the path difference
.
First, the optimal circular order C is
calculated with a TSP algorithm. The sequences are renamed with
respect to that order. Starting with the optimal circular order
C, each of the n-1 pairs of neighboring leaves are swapped
(see Algorithm 4.1.1) and the path difference
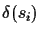 is calculated for i = 1..n. To save computation
time, we initially calculate all n
is calculated for i = 1..n. To save computation
time, we initially calculate all n
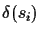 ,
sort them, and
store them in a list D.
The best connection is the one with the smallest
,
sort them, and
store them in a list D.
The best connection is the one with the smallest
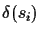 :
:
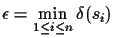 .
The
leaves are connected, and one of the connected leaves is chosen as
a representative for the next steps. For the next connection step
only two path differences
.
The
leaves are connected, and one of the connected leaves is chosen as
a representative for the next steps. For the next connection step
only two path differences 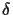 have to be recalculated, since
nothing else has changed.
Since there are n-2 internal nodes (without the root), the total
computation needs
have to be recalculated, since
nothing else has changed.
Since there are n-2 internal nodes (without the root), the total
computation needs
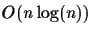 for the sorting and linear time
in n for the actual tree construction. Once the tree structure
is known the exact places of the nodes can be obtained with any
least squares method [4,21,12], which
takes in the order of n2 time. So given a circular order C,
the tree topology can be determined in
for the sorting and linear time
in n for the actual tree construction. Once the tree structure
is known the exact places of the nodes can be obtained with any
least squares method [4,21,12], which
takes in the order of n2 time. So given a circular order C,
the tree topology can be determined in
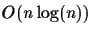 time. If the
edge lengths are to be computed as well, then the computation
takes O(n2) time. When only the input sequences are given,
then the overall computation time when only input sequences are
given is determined by the TSP algorithm.
time. If the
edge lengths are to be computed as well, then the computation
takes O(n2) time. When only the input sequences are given,
then the overall computation time when only input sequences are
given is determined by the TSP algorithm.



Next: Examples
Up: Idea of the algorithm
Previous: Idea of the algorithm
Chantal Korostensky
1999-07-14
