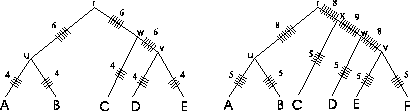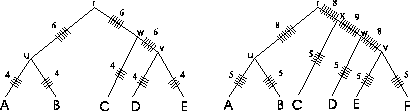Next: Traveling Salesman
Up: Methods
Previous: Methods
The sum of pairs (SP) measure is a well known scoring function for
MSAs [3,18,19,25]. We introduce the SP
measure to show our motivation to find a better scoring function
for MSAs. The connection to evolutionary trees will be clear after
the following paragraph.
To calculate the score of an MSA with the SP measure
[3], all
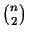 scores of the pairwise
alignments are added up. SP methods are obviously deficient from
an evolutionary perspective. Consider a tree (Figure
1) constructed for a family containing five
proteins. The score of a pairwise alignment
scores of the pairwise
alignments are added up. SP methods are obviously deficient from
an evolutionary perspective. Consider a tree (Figure
1) constructed for a family containing five
proteins. The score of a pairwise alignment
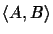 evaluates the probability of evolutionary events
on edges (u, A) and (u, B) of the tree; that is, the edges that represent
the evolutionary distance between sequence A and sequence B.
Likewise, the score of a pairwise alignment
evaluates the probability of evolutionary events
on edges (u, A) and (u, B) of the tree; that is, the edges that represent
the evolutionary distance between sequence A and sequence B.
Likewise, the score of a pairwise alignment
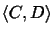 evaluates the probability of evolutionary events on edges (C,
w), (w, v) and (v, D) of the tree. The
edge lengths correspond to the PAM distances.
evaluates the probability of evolutionary events on edges (C,
w), (w, v) and (v, D) of the tree. The
edge lengths correspond to the PAM distances.
Figure 1:
Traversal of a trees using the SP
measure. Some edges are traversed more often than others. The numbers indicate how often
an edge was traversed.
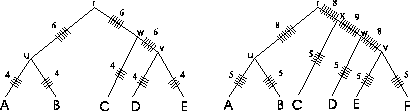 |
By adding ``ticks'' to the evolutionary tree that are drawn each
time an edge is evaluated when calculating the SP score (Figure
1), it is readily seen that with the SP method
different edges of the evolutionary tree of the protein family are
counted a different numbers of times. In the example tree on the
left side, edges (r, u), (r, w) and (w, v) are each counted
six times by the SP method, while edges (u, A), (u, B), (v,
D), (v, E), and (w, C) are each counted four times (numbers on the edges in Figure 1). It gets
worse as the tree grows (see tree on the right).
Thus, SP methods are intrinsically problematic from an
evolutionary perspective for scoring MSAs. This was the
motivation to developed a scoring method that evaluates each edge
equally. In addition, we wanted a scoring function for MSAs that
does not depend on the actual tree structure. How this can be
achieved is explained in the next section.



Next: Traveling Salesman
Up: Methods
Previous: Methods
Chantal Korostensky
1999-07-14