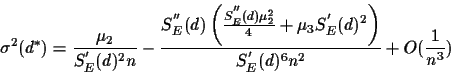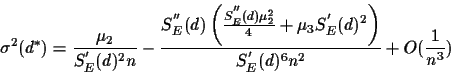Next: Degrees of Freedom
Up: Deriving the Optimal Scoring
Previous: Expected value of the
The variance
![$ \sigma^2(d^*) = E[(d^* - E[d^*])^2]$](img39.gif) can be derived
as follows. With the asymptotic value of E[d*] we compute the
Taylor series of
(d* - E[d*])2 in powers of
(w/n - SE(d)).
Then we take expected values, replacing the powers of
(w/n -
SE(d))k by the central moments described in equations
8, 9 and 10. Truncating after two
terms we obtain
can be derived
as follows. With the asymptotic value of E[d*] we compute the
Taylor series of
(d* - E[d*])2 in powers of
(w/n - SE(d)).
Then we take expected values, replacing the powers of
(w/n -
SE(d))k by the central moments described in equations
8, 9 and 10. Truncating after two
terms we obtain
The most effective estimator is the one among all possible
estimators, which has minimal variance.
The variance is
where
 .
We can compute E so that it minimizes F(d).
This will give us asymptotically (in
n) optimal estimators. We have several choices for the
minimization: we can derive the best E for
.
We can compute E so that it minimizes F(d).
This will give us asymptotically (in
n) optimal estimators. We have several choices for the
minimization: we can derive the best E for
- a given distance d, e.g.
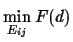 .
.
- a norm for a range of distances,
e.g. for d=0 to 200, i.e.
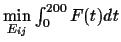 .
.
- the minimax for a range of distances, e.g. for d=0 to 200,
i.e
 .
.
There is no hope of finding a closed formula for this optimal
E, but the first and second cases can be computed numerically
without much difficulty.



Next: Degrees of Freedom
Up: Deriving the Optimal Scoring
Previous: Expected value of the
Chantal Korostensky
1999-07-14