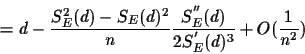Next: Variance of the estimator
Up: Deriving the Optimal Scoring
Previous: Deriving the Optimal Scoring
O( (w/n - SE(d))3)
Simplifying SE-1 and its derivatives we can rewrite the
above equation as
Taking expected values we find that
since
E[w/n - SE(d)] = E[w/n] - SE(d) = 0. When
 then
then
![$E[d^*] \rightarrow d$](img38.gif) ,
and hence
E[d*] is a consistent estimator (we could correct it to any
order of n if desired).
,
and hence
E[d*] is a consistent estimator (we could correct it to any
order of n if desired).
Chantal Korostensky
1999-07-14
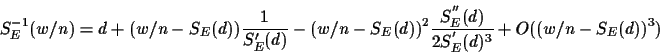
![\begin{displaymath}E[d^*] = d + E[w/n - S_E(d)] \frac{1}{S_E'(d)}-
E[(w/n - S_...
...2] \frac{S_E^{''}(d)}{2 S_E^{'}(d)^3} +
O(\frac{\mu_2}{n^2}) \end{displaymath}](img35.gif)