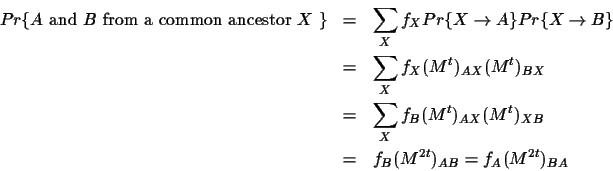Dayhoff Scores and Evolutionary Trees

There are many tree construction methods based on PAM distances [7,8,10,11,2]. PAM distances are known to be consistent, that is, the more reliable the distances are (usually when more data is available), the more reliable the tree construction is. If an infinite amount of data would be available, then the correct evolutionary tree could be constructed [4,6]. A question usually posed is: can scores derived from pairwise sequence alignments be used for evolutionary tree construction? Are they consistent? To compute scores for aligning sequences, the mutation matrix is transformed into a matrix termed a Dayhoff matrix. The Dayhoff matrix D is related to a 250-PAM mutation matrix by

$$D_{AB} = 10 \cdot \log_{10} \frac{(M^{250})_{AB}}{f_A}$$

The entries in the Dayhoff matrices are the logarithm of the probability that the two amino acids evolved from a common ancestor as opposed to being random sequences. This results from the comparison of two events (see Figure 1):

a)

the two sequences are independent of each other. Hence an arbitrary position with amino acid A aligned to another arbitrary position with amino acid B has the probability equal to the product of the individual frequencies

$$Pr \{ \mbox{independent alignment of $A$\space and $B$ } \} = f_A f_B$$

b)

the two sequences have evolved from some common ancestral sequence after some amount t of evolution.

$$\begin{eqnarray*}Pr \{ \mbox{$A$\space and $B$\space from a common ancestor $X$ ... ...{AX} (M^t)_{XB} \\ & = & f_B (M^{2t})_{AB} = f_A (M^{2t})_{BA} \end{eqnarray*}$$

$$D_{AB} = 10 \log_{10} \left ( \frac { Pr \{ \mbox{$A$\space a... ... \mbox{$A$\space and $B$\space are independent} \} } \right )$$