


Next: Deriving the Optimal Scoring
Up: Dayhoff Scores and Evolutionary
Previous: How to Make Scores
A completely generic scoring function is
S(<a,b>) = G( Ea1b1, Ea2b2, ... )
where E is a
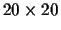 arbitrary symmetric matrix and G
is an arbitrary function which is symmetric in all its arguments.
The symmetry of E is needed because when we inspect a mutation
we cannot distinguish which mutated from which. Hence assigning
different values to Eij and Eji is biologically
incorrect. The symmetry of G is required because each mutation
is unrelated to any other and does not depend on its position in
the alignment. Therefore G depends only on the number of values
Eij for each i and j.
A brute force proof shows that for any symmetric polynomial of
degree at most 3, the most efficient estimator is the same as for
the linear case. At this time we are unable to prove that this
holds for an arbitrary degree or for an arbitrary function, but we
conjecture that the linear estimator (equation 6) is
optimal for any symmetric function. Notice that it should be
possible to approximate any reasonable estimator by an arbitrary
degree polynomial, hence we conjecture that the estimator
described here is optimal among all reasonable functions
G.
arbitrary symmetric matrix and G
is an arbitrary function which is symmetric in all its arguments.
The symmetry of E is needed because when we inspect a mutation
we cannot distinguish which mutated from which. Hence assigning
different values to Eij and Eji is biologically
incorrect. The symmetry of G is required because each mutation
is unrelated to any other and does not depend on its position in
the alignment. Therefore G depends only on the number of values
Eij for each i and j.
A brute force proof shows that for any symmetric polynomial of
degree at most 3, the most efficient estimator is the same as for
the linear case. At this time we are unable to prove that this
holds for an arbitrary degree or for an arbitrary function, but we
conjecture that the linear estimator (equation 6) is
optimal for any symmetric function. Notice that it should be
possible to approximate any reasonable estimator by an arbitrary
degree polynomial, hence we conjecture that the estimator
described here is optimal among all reasonable functions
G.



Next: Deriving the Optimal Scoring
Up: Dayhoff Scores and Evolutionary
Previous: How to Make Scores
Chantal Korostensky
1999-07-14