Discussion

We have defined a new scoring function, called CS measure, for the evaluation of MSAs that is based on a Markovian model of evolution. The frequently used SP measure, which calculates the sum of the scores of all pairwise alignments, ignores the structure of any associated phylogenetic tree and thus weights some evolutionary events more than others. This can be avoided by traversing the tree in a circular order, where all edges are traversed exactly twice. Any other non-circular tour results in a longer path, because some edges are traversed more than twice, and hence some evolutionary events are counted more often, which corresponds to a lower probability. Therefore the shortest cycle through the tree, which is a circular tour, yields the highest CS score. Such a tour can be calculated with any TSP algorithm. The The TSP application allows us to avoid the calculation of an evolutionary tree altogether, and only the sequences at the leaves are needed with their OPA or MPA scores. In addition, the CS measure yields a direct connection between an MSA and the associated evolutionary tree, because the formula for the calculation of the score is exactly the same. The CS measure based on the OPA scores gives an upper bound on the score of the optimal MSA and evolutionary tree. To illustrate the new scoring tool we simulated evolution by generating random trees according to a Markovian model with the corresponding MSA. The CS score of the generated alignment was then compared to the score of alignments calculated by different methods (MSA, ClustalW, PAS, and MAP). For less than twenty sequences MSA and PAS gave the best score, whereas for larger samples PAS and ClustalW calculated the best alignments. A better assessment must come with actual experimental sequence data though. With the new CS measure we have now the possibility of improving current algorithms and finding new algorithms by maximizing the scoring function. The most simple (and expensive) approach would be a standard dynamic programming algorithm. An approximation algorithm is presented in [Korostensky and Gonnet, 1999a] that calculates an MSA which is within 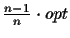$\frac{n-1}{n} \cdot opt$ (where opt is the optimal score). The CS scoring function can also be used for evolutionary trees, and a tree construction algorithm that is presented in [Korostensky and Gonnet, 1999b]. The algorithms have been implemented into the Darwin system [Gonnet, 1994b] an are available via our cbrg server at:

http://cbrg.inf.ethz.ch