Example

From a random evolutionary tree with 8 leaves a random MSA was produced, that is, the original sequence was mutated and in this case there were two indel events:

Generated random MSA:
---------------------------------------------
Score of the alignment (MPA): 1311.907
Maximum possible score (OPA): 1328.206

1       LETIDICKGCAALEYYRGPMIMRAMTSFRLDIKQQVGTTKACADATSNELTGAKLLHISDGQDTTIGQTVAIT
2       LELIDIEKGCAALEYNKGSMIMRAMTTFRLDLKDQVGSTAACADATKNKLTGAKLLHLSDGQESAMGQVVAIT
6       LHVIDERKRLEAARFNKGSVYLR___HVEIDLRTQVGSSPYAATVIKNVIKNTRPLKLCMGQELSLGMIVMLF
5       LHVIDERKRLPAARFNKGSVILK___HLEIDFQSSVGSNPRAATYVKNVIKGRKPLKLCDGQEISLGLIVCIW
7       LAVIEVRRGQVALEFNKGSVLLR___TLELDFQGQVGTPPRAAVYVKNVTKGAKPLHLVEGQEFNLGYVTCII
8       VHVADVTRGLTRLEFDKGSVVLR___HFELDFEGQAETNPRSSVYVKNVSQGVEPIHLTEWQEFNYGNVSCKI
3       LDVLDVTT___________IIIQ___TFRIDLQEQLGSNPASATYVKNILTGAKLLHLSEGEEYTMGHAVLIM
4       LDVLDVVT___________IIVV___TFRIDLQEQVGENPASASYVQDILTGAKLLHLSDGKEYTMGHVVAII

  

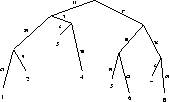
Figure 11: Tree associated with example MSA

The score of the alignment is the MPA score introduced above. It is the score derived from the pairwise alignments within the MSA, in TSP order. In this example the order is 1, 2, 6, 5, 7, 8, 3, 4. You can easily verify that this tour is a circular tour of the tree in Figure 11. The numbers on the edges of the tree are PAM distances. The maximum possible score, the CS_max(S) score (see Definition 2.4), is slightly better than the score derived from the alignment (using MPA scores). This means that the real alignment is not optimal, and the gaps could probably be shifted a bit to either side to increase the score. The indel events are one deletion event that happened in the ancestor of sequence 3 and 4 and one insertion event that happened in the ancestor of sequences 1 and 2.
Note that when the gaps are scored, each indel event is scored only once. When sequence 8 is aligned against sequence 3, the gap is scored. But when the alignment of sequences 3 and 4 is scored in the MSA, the gap scores 0, because it has already been accounted for, and you could actually simply remove the gap in the MPA (see Definition 2.6), since they have exactly the same length. Another observation is that the gaps form ``blocks'', that is, the gaps that belong to the same evolutionary event are not interrupted with sequences without gaps. The sequences at the leaves are then fed to different algorithms. None of the algorithms knows the correct tree or the correct MSA.

Sequences:
----------
1 LETIDICKGCAALEYYRGPMIMRAMTSFRLDIKQQVGTTKACADATSNELTGAKLLHISDGQDTTIGQTVAIT
2 LELIDIEKGCAALEYNKGSMIMRAMTTFRLDLKDQVGSTAACADATKNKLTGAKLLHLSDGQESAMGQVVAIT
3 LDVLDVTTIIIQTFRIDLQEQLGSNPASATYVKNILTGAKLLHLSEGEEYTMGHAVLIM
4 LDVLDVVTIIVVTFRIDLQEQVGENPASASYVQDILTGAKLLHLSDGKEYTMGHVVAII
5 LHVIDERKRLPAARFNKGSVILKHLEIDFQSSVGSNPRAATYVKNVIKGRKPLKLCDGQEISLGLIVCIW
6 LHVIDERKRLEAARFNKGSVYLRHVEIDLRTQVGSSPYAATVIKNVIKNTRPLKLCMGQELSLGMIVMLF
7 LAVIEVRRGQVALEFNKGSVLLRTLELDFQGQVGTPPRAAVYVKNVTKGAKPLHLVEGQEFNLGYVTCII
8 VHVADVTRGLTRLEFDKGSVVLRHFELDFEGQAETNPRSSVYVKNVSQGVEPIHLTEWQEFNYGNVSCKI

TSP ordering of sequences:
--------------------------
[1, 2, 6, 5, 7, 8, 3, 4, 1]

First, the sequences were fed to the MSA algorithm, which produces the following output:

MSA:
---
Score of the alignment (MPA): 1305.050
Maximum possible score (OPA): 1328.206

1       LETIDICKGCAALEYYRGPMIMRAMTSFRLDIKQQVGTTKACADATSNELTGAKLLHISDGQDTTIGQTVAIT
2       LELIDIEKGCAALEYNKGSMIMRAMTTFRLDLKDQVGSTAACADATKNKLTGAKLLHLSDGQESAMGQVVAIT
6       LHVIDERKRLEAARFNKGSVYLR___HVEIDLRTQVGSSPYAATVIKNVIKNTRPLKLCMGQELSLGMIVMLF
5       LHVIDERKRLPAARFNKGSVILK___HLEIDFQSSVGSNPRAATYVKNVIKGRKPLKLCDGQEISLGLIVCIW
7       LAVIEVRRGQVALEFNKGSVLLR___TLELDFQGQVGTPPRAAVYVKNVTKGAKPLHLVEGQEFNLGYVTCII
8       VHVADVTRGLTRLEFDKGSVVLR___HFELDFEGQAETNPRSSVYVKNVSQGVEPIHLTEWQEFNYGNVSCKI
3       LDVLDV___________TTIIIQ___TFRIDLQEQLGSNPASATYVKNILTGAKLLHLSEGEEYTMGHAVLIM
4       LDVLDV___________VTIIVV___TFRIDLQEQVGENPASASYVQDILTGAKLLHLSDGKEYTMGHVVAII

The alignment looks very similar to the constructed MSA. The only difference is that the gaps appear in different places, and the score is slightly lower than the score of the constructed MSA. In the simulation, the difference of the upper bound - the CS score were noted (see tables). In this case the difference would be 23.156. The next algorithm is the probabilistic model. In this case the algorithm merges the two gaps:

Probabilistic model:
-------------------
Score of the alignment (MPA): 1305.080
Maximum possible score (OPA): 1328.206

1       LETIDICKGCAALEYYRGPMIMRAMTSFRLDIKQQVGTTKACADATSNELTGAKLLHISDGQDTTIGQTVAIT
2       LELIDIEKGCAALEYNKGSMIMRAMTTFRLDLKDQVGSTAACADATKNKLTGAKLLHLSDGQESAMGQVVAIT
6       LHVIDERKRLEAARFNKGS___VYLRHVEIDLRTQVGSSPYAATVIKNVIKNTRPLKLCMGQELSLGMIVMLF
5       LHVIDERKRLPAARFNKGS___VILKHLEIDFQSSVGSNPRAATYVKNVIKGRKPLKLCDGQEISLGLIVCIW
7       LAVIEVRRGQVALEFNKGS___VLLRTLELDFQGQVGTPPRAAVYVKNVTKGAKPLHLVEGQEFNLGYVTCII
8       VHVADVTRGLTRLEFDKGS___VVLRHFELDFEGQAETNPRSSVYVKNVSQGVEPIHLTEWQEFNYGNVSCKI
3       LDVLDVTT______________IIIQTFRIDLQEQLGSNPASATYVKNILTGAKLLHLSEGEEYTMGHAVLIM
4       LDVLDVVT______________IIVVTFRIDLQEQVGENPASASYVQDILTGAKLLHLSDGKEYTMGHVVAII

The last algorithm tested in this example is ClustalW. It looks like the algorithm also found two indel events, but when you look closer you can see that the gaps are shifted against each other. This means that the second block of gaps are two indel events and not just one, which is the reason for the lower score.

ClustalW:
---------
Score of the alignment (MPA): 1291.417
Maximum possible score (OPA): 1328.206

1       LETIDICKGCAALEYYRGPMIMRAMTSFRLDIKQQVGTTKACADATSNELTGAKLLHISDGQDTTIGQTVAIT
2       LELIDIEKGCAALEYNKGSMIMRAMTTFRLDLKDQVGSTAACADATKNKLTGAKLLHLSDGQESAMGQVVAIT
6       LHVIDERKRLEAARFNKGSVYLR___HVEIDLRTQVGSSPYAATVIKNVIKNTRPLKLCMGQELSLGMIVMLF
5       LHVIDERKRLPAARFNKGSVILK___HLEIDFQSSVGSNPRAATYVKNVIKGRKPLKLCDGQEISLGLIVCIW
7       LAVIEVRRGQVALEFNKGSVLLR___TLELDFQGQVGTPPRAAVYVKNVTKGAKPLHLVEGQEFNLGYVTCII
8       VHVADVTRGLTRLEFDKGSVVLR___HFELDFEGQAETNPRSSVYVKNVSQGVEPIHLTEWQEFNYGNVSCKI
3       LDVLDVTT___________III___QTFRIDLQEQLGSNPASATYVKNILTGAKLLHLSEGEEYTMGHAVLIM
4       LDVLDVVT___________IIV___VTFRIDLQEQVGENPASASYVQDILTGAKLLHLSDGKEYTMGHVVAII

Following is the result of a large simulation. For each tree type hundreds of alignments were produced. This is the reason why the scores have variances, because the upper bound is not the same for each set of sequences, but lies in the same order, because similar PAM distances were used and the same underlying tree structure. Higher scores or smaller differences mean better alignments. The rows are sorted into ascending order. Figure 12 shows the result for balanced binary trees with 16 leaves. The length of the sequences is 300 amino acids and the average edge distance is 30 PAM (so the maximum PAM distance between two sequences is about 240 PAM).

  

Figure 12: Comparison of different MSA methods: the CS score (second column) is calculated using a TSP ordering. The upper bound is the CS score based on the optimal pairwise alignment.

Method	CS Score	Upper bound - CS score
Upper bound:	22451 $\pm$ 516	0
MSA:	21767 $\pm$ 513	684 $\pm$ 76
PAS	21414 $\pm$ 481	740 $\pm$ 74
Real:	21367 $\pm$ 439	781 $\pm$ 74
ClustalW:	21330 $\pm$ 473	822 $\pm$ 76
MAP:	18633 $\pm$ 608	3521 $\pm$583
Dummy:	5948 $\pm$ 911	16200 $\pm$ 826

For this tree, MSA scored the best followed by PAS, ClustalW and MAP. The alignments of MSA and PAS are slightly better than the ``real'' alignment. The reason for this is that the simulated MSAs are not necessarily optimal. As a comparison the score of a bad alignment (all the sequences aligned without deletions) was calculated in the last row (Dummy). The tree on the right is an example of a generated phylogenetic tree. The next trees (Figure 13) are unbalanced with 30 sequences of length 300 and the average edge distance is 30 PAM (so the maximum PAM distance is about 300). Only PAS, MAP and ClustalW were able to compute the alignments (in a reasonable time). In this case PAS did slightly better than ClustalW.

  

Figure 13: Comparison of different MSA methods: the CS score (second column) is calculated using a TSP ordering. The upper bound is the CS score based on the optimal pairwise alignment.

Method	CS Score	Upper bound - CS score
Upper bound:	40282$\pm$ 581	0
Real:	38796$\pm$ 573	1486 $\pm$ 138
PAS	38638$\pm$ 594	1643 $\pm$ 151
ClustalW:	38465$\pm$ 597	1818 $\pm$ 153
MAP	21238$\pm$ 1565	18957$\pm$ 1507
Dummy:	10609$\pm$ 1321	28641$\pm$ 1308

The trees of the last table shown here (Figure 14) had 50 sequences with length 300 and an average edge length of 15 PAM. In the simulation the PAS method was the best followed by ClustalW. No other methods were able to calculate an MSA in a reasonable time.

  

Figure 14: Comparison of different MSA methods: the CS score (second column) is calculated using a TSP ordering. The upper bound is the CS score based on the optimal pairwise alignment.

Method	CS Score	Upper bound - CS score
Upper bound:	91232$\pm$ 924	0
Real:	88960 $\pm$ 913	2272 $\pm$ 167
PAS:	88494 $\pm$ 941	2704 $\pm$ 175
ClustalW:	87313 $\pm$ 1654	3884 $\pm$ 1363
Dummy:	34062 $\pm$ 4558	57456$\pm$3954

These experiments show how the CS measure can be used. It also shows that the upper bound CS_max(S) is very close to the actual score 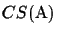$CS(\mbox{\rm A})$ of the simulated MSA. Obviously the ultimate evaluation of tools must be done with real rather than simulated data.