


Next: Traveling Salesman Problem Application
Up: Methods
Previous: Methods
Definition 2.1
A
Circular order C(
T) of set of sequences
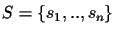
is any
tour through a tree
T(
S) where each edge is traversed exactly twice,
and each leaf is visited once.
The problem can be solved by walking through the tree in a
circular order, that is, from leaf A to B, from B to C, from C to
D, from D to E and then back from E to leaf A (Figure
3), all edges are counted exactly twice, independent of
the tree structure.
Figure 3:
Traversal of a tree in circular order
 |
Lemma 2.1 (Shortest Tour)
The circular tour is the shortest possible tour through a tree
that visits each leaf once (see Figure
3). It traverses
all edges exactly twice and thus weights all edges of the
evolutionary tree equally.
Proof 2.1
Starting with 2 leaves, the proof is obvious: there is only one
tour and all edges are counted exactly twice (see Figure
4).
Figure 4:
circular tour for 2 leaves
 |
When we have a tree with
n leaves, subdivide the tree anywhere
into the subtrees
sA and
sB (see Figure
5)
and look at the edge
x in the middle that connects the two
subtrees. When the tree is traversed in the order

and back to 1 in a circular tour, edge
x is traversed exactly twice. Since the division into subtrees
can be done anywhere in the tree, all edges are counted twice.
There is no shorter tour, because we have to come back to the
first leaf.
Figure 5:
circular tour for n leaves
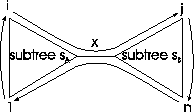 |
Lemma 2.2 (Non-circular Tours)
Any other non-circular tour traverses at least one
edge more than twice.
Proof 2.2
Again take a tree with
n leaves, and subdivide the tree anywhere
into the subtrees
sA and
sB (see Figure
6).
When the tree is traversed in the order
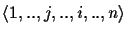
and back to 1 (so we first go to
j and then to
i),
edge
x in the middle is traversed four times.
Figure 6:
Non-circular tour for n leaves
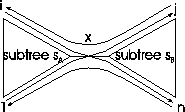 |
For each tree T there exist 2(n-2) isomorphic forms. An isomorphic
tree T' has the same tree topology as T, and it differs from T
only in the sense that a subtree is rotated (in a graphical
representation).
Lemma 2.3 (Isomorphic Trees)
A circular tour
C(
T) of a tree
T is also a circular tour for
all isomorphic trees of T.
Proof 2.3
Take the same tree as in Figure
5, but this time
rotate one of the subtrees (leaves
j and
n are now on the
opposite side as before)(see Figure
7). When the
tree is traversed again in the order

and back to 1, the middle edge is only traversed twice.
Again, since the division into subtrees can be done anywhere in
the tree, all edges are counted twice, therefore this is true for
all isomorphic trees.
Figure 7:
circular tour of an isomorphic tree
 |
An immediate conclusion from this is that any tree has 2(n-2)
different circular tours which correspond to the circular orders
of the isomorphic trees.
Definition 2.2
A tour
Ci is
shorter than a tour
Cj (
Ci <
Cj) if the number of
edges that are traversed by
Ci is larger than the number of
edges that are traversed by
Cj.
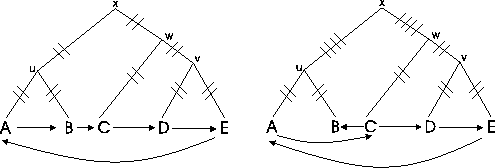
Example 2.1:The order
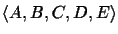 is a circular
order in Figure 8, but not
is a circular
order in Figure 8, but not
 .
In the second example, edges
.
In the second example, edges
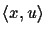 and
and
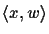 are counted four times, while all
other edges are counted only twice.
are counted four times, while all
other edges are counted only twice.
Figure:
Traversal of a phylogenetic tree in a
circular
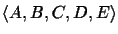 and non-circular order
and non-circular order

 |



Next: Traveling Salesman Problem Application
Up: Methods
Previous: Methods
Chantal Korostensky
1999-07-14