Introduction

Several structure prediction methods and methods for evolutionary tree construction are based on multiple sequence alignments (MSAs) [1,2,3,4,5,6,7,8,9]. The quality of an MSA highly influences the outcome of structure prediction. As a first step the MSA is scanned for parse regions. Parses are regions in the protein between secondary structures ($\alpha-$helices or $\beta-$sheets), such as loops. Usually gaps (insertions or deletion events) indicate parses. This is the most important step for assigning parses, and misplaced gaps are problematic for structure prediction, because once a parse region is chosen, no other secondary structures can traverse that position anymore. The problem of calculating MSAs can be viewed as the problem of inserting gaps at the correct places. There are many MSA algorithms [11,12,13,14,15], but none of them produce optimal alignments (for realistic instances of the problem) due to the complexity (the common models for calculating MSAs in are known to be NP-complete [10]). In this paper we present two different algorithms for dealing with misplaced gaps in MSAs. The first algorithm improves given MSAs by reducing the number of evolutionary events. The second algorithm shows how to build an evolutionary tree from an MSA where misplaced gaps prevent a unique solution. Gaps play a special role both in terms of structure and evolution (see following sections). This fact can be used to improve MSAs and to construct the corresponding evolutionary tree. It is important to develop algorithms that use as much biological information as possible, such that structure prediction and evolutionary tree construction based on MSAs become more reliable.

  

Figure: The sequences $\langle A, B, C, D, E\rangle$ of the MSA on the left are related by the evolutionary tree on the right. The internal nodes in the tree represent unknown ancestor sequences.

A: RPCVCP___VLRQAAQ__QVLQRQIIQGPQQLRRLF_AA B: RPCACP___VLRQVVQ__QALQRQIIQGPQQLRRLF_AA C: KPCLCPKQAAVKQAAH__QQLYQGQLQGPKQVRRAFRLL D: KPCVCPRQLVLRQAAHLAQQLYQGQ____RQVRRAF_VA E: KPCVCPRQLVLRQAAH__QQLYQGQ____RQVRRLF_AA

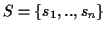
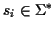
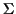
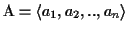
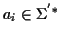
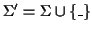
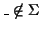
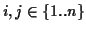
Definition 1.1   Given is a set of sequences $S = \{s_1, .., s_n\}$ with $s_i \in \Sigma^*$ where $\Sigma$ is a finite alphabet. A Multiple Sequence Alignment (in short, MSA) consists of a set of sequences $\mbox{\rm A}= \langle a_1, a_2, .., a_n\rangle$ with $a_i \in \Sigma^{'*}$ where $\Sigma' = \Sigma \cup \{\_\}$, $\_ \not \in \Sigma$. Furthermore |a_i|=|a_j| for all $i,j \in \{1..n\}$. 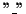The sequence obtained by removing all gap $''\_''$ characters from a_i is equal to s_i.

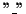
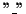
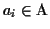
Definition 1.2   The character $''\_''$ or any contiguous sequence of $''\_''$ within an aligned sequence $a_i \in \mbox{\rm A}$ is called a gap. A gap corresponds to an insertion or deletion event (indel). The length of a gap |g| is the number of $''\_''$.

Definition 1.3   A tree T(S)=(V, E, L) is a binary, leaf-labeled tree with vertices V, edges E and leaf labels $L = \{s_1, .., s_n\}$.

In our context, for a set of sequences $S = \{s_1, .., s_n\}$ the tree T(S) is the tree that corresponds to the evolutionary history of the sequences of S. The internal nodes V represent the (usually unknown) ancestor sequences.

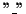
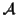
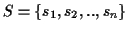
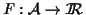
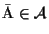
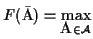
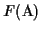
Definition 1.4   Let $\cal{A}$ be the set of all possible MSAs that can be generated for a given set of sequences $S=\{s_1, s_2, .., s_n\}$. An MSA scoring function $F: \cal{A} \rightarrow I \!\! R$ is a function, where a larger value corresponds to a better alignment (otherwise the function can be multiplied by -1). The optimal MSA $\bar{\mbox{\rm A}} \in \cal{A}$ is an MSA such that $F(\bar{\mbox{\rm A}}) = \max\limits_{\mbox{\rm A}\in \cal{A}}$ $F(\mbox{\rm A})$.