


Next: Progressive Alignment:
Near Optimal Multiple Sequence Alignments Using a Traveling Salesman Problem Approach
Chantal Korostensky and Gaston Gonnet
Swiss Federal Institute of Technology
Institute of Scientific Computing
ETH Zürich, Switzerland
korosten, gonnet@inf.ethz.ch
Abstract:
We present a new method for the calculation of multiple sequence
alignments (MSAs). The input to our problem are
n protein
sequences. We assume that the sequences are related with each
other and that there exists some unknown evolutionary tree that
corresponds to the MSA. One advantage of our method is that the
scoring can be done with reference to this phylogenetic tree, even
though the tree structure itself may remain unknown. Instead of
computing an evolutionary tree, we only need to compute a circular
tour of the tree which is determined via a Traveling Salesman
Problem (TSP) algorithm. Our algorithm can calculate a near
optimal MSA and has a performance guarantee of

(where
opt is the optimal score of the MSA). The algorithm
runs in
O(
k2 n2) time, where
k is the length of the longest
input sequence. From there we improve the alignment further.
Experimental results are shown at the end.
Introduction The computation of multiple
sequence alignments (MSAs) remains one of the major open problems
in computational biology. Possibly this is due to the complexity
as most problems associated with MSAs are NP-complete
[20]. It is therefore desirable to develop heuristics
that try to come as close to the optimum as possible but terminate
within reasonable time and space bounds. An MSA consists of a set
of strings, where each string represents an amino acid, DNA or RNA
sequence (see Definition 1.1).
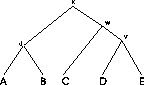
Figure:
The sequences
 of the MSA on the left are related by the evolutionary tree on the
right.
of the MSA on the left are related by the evolutionary tree on the
right.
A: RPCVCP___VLRQAAQ__QVLQRQIIQGPQQLRRLF_AA
B: RPCACP___VLRQVVQ__QALQRQIIQGPQQLRRLF_AA
C: KPCLCPKQAAVKQAAH__QQLYQGQLQGPKQVRRAFRLL
D: KPCVCPRQLVLRQAAHLAQQLYQGQ____RQVRRAF_VA
E: KPCVCPRQLVLRQAAH__QQLYQGQ____RQVRRLF_AA
|
 |
|
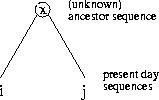
Example: In the MSA in Figure
1 five sequences are aligned (n=5). We
assume that the sequences are related and that we have the correct
tree. The internal nodes represent unknown ancestor sequences.
Definitions
Definition 0.1
Given is a set of sequences
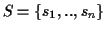
with
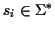
where
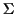
is a finite alphabet. A
Multiple
Sequence Alignment (MSA) consists of a set of sequences
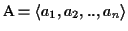
with
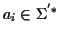
where
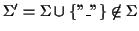
.
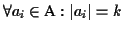
.
The sequence obtained from
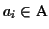
by removing all
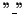
gap characters is equal to
si.
Definition 0.2
The character
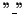
or any contiguous sequence of
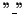
within an aligned sequence
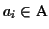
is called a
gap. A gap
g has length
len(
g), where the
length is the number of contiguous dashes
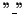
.
It starts at a position
pos(
g) in sequence
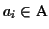
and ends at position
end(
g).
Definition 0.4
Let
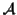
be the set of all possible MSAs that can be
generated for a given set of sequences

.
The
optimal MSA
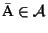
is an MSA such that
w.l.o.g.


.
In many scoring functions the minimum is the optimal.
Problem 0.1 (MSA problem)
Given is a set of sequences
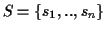
.
Find the
optimal MSA

for
S.
Scoring Pairwise Sequence Alignments To determine if
two sequences
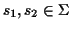 are related and have a common
ancestor the sequences are usually aligned, and the problem is to
find the alignment that maximizes the probability that the two
sequences are related:
To actually calculate these probabilities, one applies a Markovian
model for sequence evolution [25,3].
This begins with an alignment of the two sequences, e.g.
are related and have a common
ancestor the sequences are usually aligned, and the problem is to
find the alignment that maximizes the probability that the two
sequences are related:
To actually calculate these probabilities, one applies a Markovian
model for sequence evolution [25,3].
This begins with an alignment of the two sequences, e.g.
VNRLQQNIVSL____________EVDHKVANYKP
VNRLQQSIVSLRDAFNDGTKLLEELDHRVLNYKP
The gaps arise from insertions (or their counterpart
deletions) during divergent evolution. The alignment is normally
done by a dynamic programming (DP) algorithm using Dayhoff
matrices
[12,32,28,1], which
finds the alignment that maximizes the probability that the two
sequences evolved from an ancestral sequence as opposed to being
random sequences. An affine gap cost is used according to the
formula
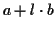 ,
where a is a fixed gap cost, l is the
length of the gap and b is the incremental cost
[1,4]. More precisely, we are comparing
two possibilities
,
where a is a fixed gap cost, l is the
length of the gap and b is the incremental cost
[1,4]. More precisely, we are comparing
two possibilities
- a)
- that the two sequences arose
independently of each other (implying that the alignment is entirely arbitrary,
with amino acid i in one protein being aligned to amino acid j
in the other is occurring no more frequently than expected by
chance, which is equal to the product of the individual
frequencies with which amino acids i and j occur in the
database)
 |
(1) |
- b)
- that the two sequences have evolved
from some common ancestral sequence after t units of evolution
where t is measured in PAM units [9].

 |
(2) |
Definition 0.5
The score of an
optimal pairwise alignment
OPA(
s1,
s2) of two
sequences
s1,
s2 is the score of an alignment with the
maximum score where a probabilistic scoring method
[
6,
10] is used. We refer to a pairwise
alignment of two sequences
s1,
s2 with
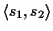
.
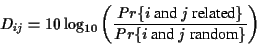 |
(3) |
The entries of the Dayhoff matrix are the logarithm of the
quotient of these two probabilities. Note that scores represent
the probabilities that the two sequences have a common ancestor.
The larger the score is the more likely it is that the two
sequences are homologous and therefore have a common ancestor.
Related work There are two main methods for finding
an optimal MSA:
- global methods which construct an alignment throughout the
length of the entire sequence (see below), and
- local methods which only attempt to identify an ordered series
of motifs (homologous regions) while ignoring regions between
motifs [17,18].
We are concerned with global methods and we briefly describe the
different strategies used along with some of their drawbacks.
Heuristics



Next: Progressive Alignment:
Chantal Korostensky
1999-07-14
