


Next: Step 2
Up: Near Optimal Multiple Sequence
Previous: Tree Alignment (TA) and
The MSA and maximum weight trace methods
[5,14,15,24] differ from
the others because they compute an optimal alignment with
respect to a well-defined MSA scoring (sum-of-pairs). This is an
exact algorithm and the running time is typically O(kn) which
is only practical for a very small number (n) and length (k) of
sequences. In addition, the scoring function
that is used does not reflect the structure of the underlying evolutionary
tree, unless the scoring function is weighted, in which case a
tree must be known (or constructed).
A better and more detailed overview of multiple sequence
alignment methods is presented in
[27,19,38].
Error Bounds and Performance
Guarantees There is a
bounded-error approximation method by Gusfield [16]
for the sum of pairs (SP) measure that calculates an MSA with
a score that is never more than twice that of the optimal SP
score. Here a scoring method is used where lower scores
correspond to better alignments.
Another bound is presented by Bafna, Lawler and Pevzner
[2]. Their method aligns n strings and produces an
MSA whose SP score can never exceed
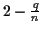 times the
optimal SP score, for any chosen q. For any fixed value of q,
the running time of the method is polynomial in k (the assumed
string length of each string) and n. As q increases, so does
the provable accuracy of the result, but the worst-case running
time also increases.
times the
optimal SP score, for any chosen q. For any fixed value of q,
the running time of the method is polynomial in k (the assumed
string length of each string) and n. As q increases, so does
the provable accuracy of the result, but the worst-case running
time also increases.
In this extended abstract we present an algorithm that runs in
O(n2 k2) time and produces an MSA whose score is at least
 .
The score of the alignment represents
the probability of the entire evolutionary configuration. In the
following sections we briefly explain the scoring function. See
[11] for a more detailed exposition. We then describe
the algorithm for the calculation of MSAs and present experimental
results.
Methods Sum of Pairs versus Circular Sum
measure
.
The score of the alignment represents
the probability of the entire evolutionary configuration. In the
following sections we briefly explain the scoring function. See
[11] for a more detailed exposition. We then describe
the algorithm for the calculation of MSAs and present experimental
results.
Methods Sum of Pairs versus Circular Sum
measure
Definition 0.6
The
tree
T(
S)=(
V,
E,
L) is a binary, leaf labeled tree
with leafset
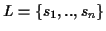
.
In our context a tree T(S) associated with a set of sequences
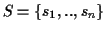 is the tree
that corresponds to the evolutionary history of the sequences of
S. The internal nodes V represent (usually unknown) ancestor sequences.
To calculate the score with the SP measure
[5], all
is the tree
that corresponds to the evolutionary history of the sequences of
S. The internal nodes V represent (usually unknown) ancestor sequences.
To calculate the score with the SP measure
[5], all
 scores of the pairwise
alignments are added up. SP methods are obviously deficient from
an evolutionary perspective. Consider a tree (Figure
2) constructed for a family containing five
proteins. The score of a pairwise alignment
scores of the pairwise
alignments are added up. SP methods are obviously deficient from
an evolutionary perspective. Consider a tree (Figure
2) constructed for a family containing five
proteins. The score of a pairwise alignment
 evaluates the probability of evolutionary events
on edges (u, A) and (u, B) of the tree; that is, the edges that represent
the evolutionary distance between sequence A and sequence B.
Likewise, the score of a pairwise alignment
evaluates the probability of evolutionary events
on edges (u, A) and (u, B) of the tree; that is, the edges that represent
the evolutionary distance between sequence A and sequence B.
Likewise, the score of a pairwise alignment
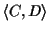 evaluates the likelihood of evolutionary events on edges (C, w),
(w, v) and (v, D) of the tree.
evaluates the likelihood of evolutionary events on edges (C, w),
(w, v) and (v, D) of the tree.
Figure 2:
Traversal of trees using the SP
measure. Some edges are traversed more often than others.
 |
By adding ``ticks'' to the evolutionary tree that are drawn each
time an edge is evaluated when calculating the SP score (Figure
2), it is readily seen that with the SP method
different edges of the evolutionary tree of the protein family are
counted a different numbers of times. In the example tree on the
left side that corresponds to the MSA of Figure
1, edges (r, u), (r, w) and (w, v) are
each counted six times by the SP method, while edges (u, A),
(u, B), (v, D), (v, E), and (w, C) are each counted four
times. It gets worse as the tree grows (see tree on the right).
There is no theoretical justification to suggest that some
evolutionary events are more important than other ones.
Thus, SP methods are intrinsically problematic from an
evolutionarily perspective for scoring MSAs. This was the
motivation to developed a scoring method that evaluates each edge
equally. In addition, we wanted a scoring function that does not
depend on the actual tree structure.
Traveling Salesman
Definition 0.7
A
Circular order

of an MSA

is any
tour through a tree
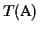
where each edge is traversed exactly twice,
and each leaf is visited once.
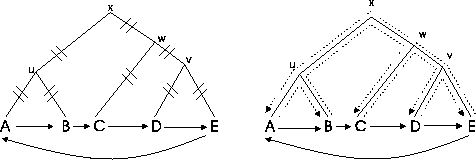
When a tree is traversed in a circular order, that is, from leaf A
to B, from B to C, from C to D, from D to E and then back from E
to leaf A (Figure 3), all edges are counted exactly
twice, independent of the tree structure. A circular order is the
shortest possible tour through a tree where each leaf is visited
once (shortest means smallest sum of edge lengths)(see Figure
3) [11]. Since we do not want to rely on any
tree, the problem we consider is to find such an order without
having any information about the tree structure.
To solve this problem we reduce it to the symmetric Traveling
Salesman Problem (TSP): given is a matrix M that contains the
 distances of n cities [23,22].
The problem is to find the shortest tour where each city is
visited once. We use a modified version of the problem: in our
case, the cities correspond to the sequences and the distances are
the scores of the pairwise alignments. In addition, we are
interested in the longest, not shortest tour, as our scores
represent probabilities and we are interested in the maximum
probability 1.
distances of n cities [23,22].
The problem is to find the shortest tour where each city is
visited once. We use a modified version of the problem: in our
case, the cities correspond to the sequences and the distances are
the scores of the pairwise alignments. In addition, we are
interested in the longest, not shortest tour, as our scores
represent probabilities and we are interested in the maximum
probability 1.
Problem 0.2 (TSP problem)
Given is a set of sequences
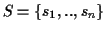
and the
corresponding scores of the optimal pairwise alignments. The
problem is to find the longest tour where each sequence is visited
once.
Figure 3:
Traversal of a tree in circular order
 |
Both the construction of optimal evolutionary trees
[8,20] and the Traveling Salesman Problem are NP
complete. But the TSP is very well studied and optimal solutions
can be calculated within a few hours for up to 1000 cities and in
a few seconds for up to 100 cities, whereas the construction of
evolutionary trees is still a big problem. There are heuristics
for large scale problems that calculate near optimal solutions
that are within 1% to 2% of the optimum
[29,13]. For real applications we have seldom
more than 100 sequences to compare simultaneously, and the
calculation of the optimal TSP solution usually takes only a small
fraction of the time it takes to compute all pairwise alignments
to derive the scores.
Definition 0.8
The
TSP order

of an MSA

is the order of the sequences
that is derived from the optimal solution of a TSP.
In summary, we can compute a circular order
 without
knowing
without
knowing
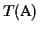 .
For a more detailed explanation see
[11].
MSA scoring function
.
For a more detailed explanation see
[11].
MSA scoring function
Definition 0.9
The function
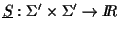
is defined as
follows:
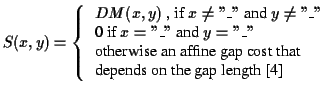
DM is an entry in the Dayhoff matrix
[
10].
Our scoring function
 of an MSA is similar to the
sum-of-pairs measure, except that we do not add all scores of all
pairwise alignments, but only the scores of the pairwise
alignments in the circular order C divided by two. It is the
sum-of-pairs in circular order:
of an MSA is similar to the
sum-of-pairs measure, except that we do not add all scores of all
pairwise alignments, but only the scores of the pairwise
alignments in the circular order C divided by two. It is the
sum-of-pairs in circular order:
where k is the length of a sequence in the MSA, n is
the number of sequences, C is the TSP ordering, aCi is a
sequence in the MSA, and so the
aCi[m] are amino acids or
gap characters within that sequence. S(x,
y) is the score of aligning the symbol
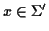 with the
symbol
with the
symbol
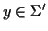 .
The function S(x, y) is defined above
(see Definition 2.4).
Circular Tours and Gaps Gaps play a special role in
MSAs: the process of calculating an MSA can be viewed as inserting
gaps at the correct places.
Assume we are given an MSA
.
The function S(x, y) is defined above
(see Definition 2.4).
Circular Tours and Gaps Gaps play a special role in
MSAs: the process of calculating an MSA can be viewed as inserting
gaps at the correct places.
Assume we are given an MSA
 and we know the correct tree
and we know the correct tree
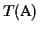 .
Insertions and deletions (indels) are evolutionary events
that can be placed in the evolutionary tree (see Figure
5). The result of a deletion event are gaps that
appear in all sequences of the subtree where the event took place.
In contrast, when the event was an insertion, gaps appear in all
sequences that are not in the subtree below the event.
.
Insertions and deletions (indels) are evolutionary events
that can be placed in the evolutionary tree (see Figure
5). The result of a deletion event are gaps that
appear in all sequences of the subtree where the event took place.
In contrast, when the event was an insertion, gaps appear in all
sequences that are not in the subtree below the event.
Definition 0.11
A
gap block B is a set of gaps
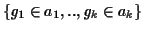
where the gaps have the following properties:
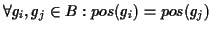
and
len(
gi) =
len(
gj).
Example: In the alignment of Figure
4, there are 4 indel events and therefore 4 gap
blocks. The first gap block consists of two gaps that appear in
sequences A and B. We assume we have the correct tree and we also
assume that we know the place of the root. In this case the event
must be a deletion in the ancestor of sequences A and B.
Accordingly, event 2 is an insertion in sequence D, event 3
represents a deletion in the ancestor of D and E, and finally
event 4 is an insertion in sequence C.
Figure 4:
An MSA and a table containing the
pairwise scores
Event 1 2 3 4
A: RPCVCP___VLRQAAQ__QVLQRQIIQGPQQLRRLF_AA
B: RPCACP___VLRQVVQ__QALQRQIIQGPQQLRRLF_AA
C: KPCLCPKQAAVKQAAH__QQLYQGQLQGPKQVRRAFRLL
D: KPCVCPRQLVLRQAAHLAQQLYQGQ____RQVRRAF_VA
E: KPCVCPRQLVLRQAAH__QQLYQGQ____RQVRRLF_AA
|
| |
A |
B |
C |
D |
E |
| A |
0 |
336 |
27 |
44 |
110 |
| B |
336 |
0 |
79 |
56 |
99 |
| C |
27 |
79 |
0 |
171 |
176 |
| D |
44 |
56 |
171 |
0 |
327 |
| E |
110 |
99 |
176 |
327 |
0 |
|
|
Figure 5:
Insertion and deletion events are
shown in the evolutionary tree.
 |
The table to the right shows the pairwise scores of the
sequences. It is easy to verify that the shortest tour is (A, B,
C, D, E, A) and that it is a circular tour in the corresponding
tree (see Figure 1). The score of the MSA is
the sum of pairwise alignments in circular order divided by two, so
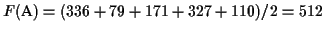 .
Here the MSA has the
optimal score.
Note that the sequences above are ordered in a
circular way
.
Here the MSA has the
optimal score.
Note that the sequences above are ordered in a
circular way
 .
Whenever sequences are in a circular
order with respect to the evolutionary tree, the gaps that belong
to the same evolutionary event appear in a gap block (ignoring the
breaking of the circularity).
Results The fact that gaps originating from the same
event form gap blocks if a circular tour is known simplifies the
task of calculating an MSA.
.
Whenever sequences are in a circular
order with respect to the evolutionary tree, the gaps that belong
to the same evolutionary event appear in a gap block (ignoring the
breaking of the circularity).
Results The fact that gaps originating from the same
event form gap blocks if a circular tour is known simplifies the
task of calculating an MSA.
Figure 6:
Schematic representation of an
MSA in a circular order
 |
In Figure 6, a schematic representation of an
MSA is shown, where the vertical lines are sequences in the
alignment. The rectangles represent gap blocks, and the cylinder
itself represents the circular order of the tree.
Once a circular order
 is known, we have to select a
starting point in the cycle. In principle it does not matter where
we start, but as we will see later it is simpler if we cut the
cycle in a place where the sequences are farther apart. This is
the two sequences in the cycle with the smallest similarity score.
We then renumber the sequences with respect to the cycle starting
from that point (see Figure 6).
Algorithm
is known, we have to select a
starting point in the cycle. In principle it does not matter where
we start, but as we will see later it is simpler if we cut the
cycle in a place where the sequences are farther apart. This is
the two sequences in the cycle with the smallest similarity score.
We then renumber the sequences with respect to the cycle starting
from that point (see Figure 6).
Algorithm
Definition 0.12
Similar to the definition of the score of an MSA we define the
partial score
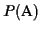
of an MSA

:
it is the
sum-of-pairs in circular order except for the last term:
![$ P(\mbox{\rm A}) = \frac{1}{2}\sum\limits_{m=1}^{k}
\sum\limits_{i=1}^{n-1} S(a_{C_{i}}[m], a_{C_{i+1}}[m])$](img53.gif)
(see
1.3).
The partial score of the MSA in Figure 4 is
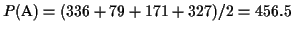 .
.
Assume we are given n sequences
 which are
ordered with respect to a circular order C. Assume further that
the first k sequences are already aligned and build an MSA
which are
ordered with respect to a circular order C. Assume further that
the first k sequences are already aligned and build an MSA
 with optimal partial
score (see Figure 7). We refer to the unaligned
input sequences with si, to the sequences in the MSA with ai
and to the sequences in an optimal pairwise alignment with ti.
with optimal partial
score (see Figure 7). We refer to the unaligned
input sequences with si, to the sequences in the MSA with ai
and to the sequences in an optimal pairwise alignment with ti.
Figure:
Sequences
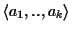 are aligned and build an MSA
are aligned and build an MSA
 with optimal
partial score.
with optimal
partial score.
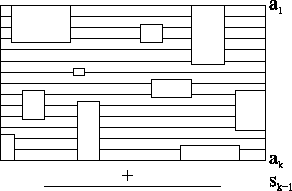 |
The algorithm has four steps:
- 1.
- take sequence sk and calculate an optimal pairwise
alignment with the next sequence sk+1. The sequences in this
alignment with the gaps are called tk and tk+1 (see Figure 8).
- 2.
- insert all gaps from tk that are not already present in ak into all
previously aligned sequences
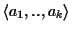 (see Figure 9).
(see Figure 9).
- 3.
- take all the gaps that were present in ak before
step 2), and insert them in both, tk and tk+1, except for the gaps that are already present in tk (see Figure 9).
- 4.
- at this point ak = tk and
ak+1 = tk+1. We
add ak+1 to the alignment and increment k by one (see Figure 9).
Figure 8:
Step 1:
 |
We now discuss steps 2 to 4 and show that in each step
the MSA has an optimal partial score:



Next: Step 2
Up: Near Optimal Multiple Sequence
Previous: Tree Alignment (TA) and
Chantal Korostensky
1999-07-14
![$ P(\mbox{\rm A}) = \frac{1}{2}\sum\limits_{m=1}^{k}
\sum\limits_{i=1}^{n-1} S(a_{C_{i}}[m], a_{C_{i+1}}[m])$](img53.gif)