Nächste Seite: 9. Einführungen in MATLAB, Aufwärts: 8. Anwendungen aus der Vorherige Seite: 8.4.3 Fitting a Rectangle Inhalt
In der Statistik kommt es oft vor, dass eine Serie von
Ausgleichsproblemen gelöst werden muss, wobei die Matrix
![]() jeweils nur wenig ändert. Wir betrachten dazu die
folgende Problemstellung:
jeweils nur wenig ändert. Wir betrachten dazu die
folgende Problemstellung:
Gegeben sei die QR-Zerlegung
![]() mit
mit
![]() . Gegeben seien ferner die Vektoren
. Gegeben seien ferner die Vektoren
![]() und
und
![]() .
.
Kann man die QR-Zerlegung der Matrix
Es ist
 mit
mitDer Algorithmus besteht aus drei Schritten:
 |
 |
|
 |

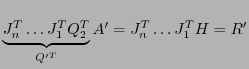
function [G ] = rot(m,i,k,x,y); % [G ] = rot(m,i,k,x,y); % konstruiert eine orthogonale Matrix G mxm, welche y zu null rotiert G = eye(m,m); if y~=0, cot = x/y; si = 1/sqrt(1+cot^2); co = si*cot; G(i,i) = co; G(k ,k) = co; G(i,k) = si; G(k,i) = -si; end;
Damit kann das folgende Programm geschrieben werden. Nach jeder Rotation wurde ein Pausenbefehl eingefügt, man kann damit den Ablauf des Algorithmus leicht verfolgen.
A= rand(7,4);
u=rand(7,1);
v=[1 2 3 4]';
[m n] = size(A);
[Q R] = qr(A);
QS =Q;
RS = R;
%
w = Q'*u
disp(' 1. Phase: Anullieren w(n+2:m) und aendern nur Q')
for i=m:-1:n+2,
G= rot(m,i-1,i,w(i-1), w(i))
w = G*w
QS = QS*G';
pause
end;
disp(' 2. Phase Annullieren w(2:n+1) und aendern R und Q')
for i= n+1:-1:2,
G= rot(m,i-1,i,w(i-1), w(i))
w = G*w
RS = G*RS
QS = QS*G';
pause
end
disp(' Addieren jetzt die Rang 1 Mod. zur ersten Zeile von R')
RS = RS + w*v'
pause
disp(' 3.Phase: RS ist nun Hessenberg und wird reduziert')
for i = 1:n,
G= rot(m,i,i+1,RS(i,i), RS(i+1,i))
RS = G*RS
QS = QS*G';
pause
end
disp(' Kontrolle')
AS = A + u*v'; [qs rs] = qr(AS);
qs
QS
rs
RS
Nun ist es einfach die Demonstrationsversion zu einem effektiven
Programm umzuschreiben. Wir benötigen dazu eine Funktion giv, um die Rotationswinkel, bzw. den ![]() und
und ![]() davon zu
berechnen:
davon zu
berechnen:
function [s,c] = giv(x,y); % bestimmt eine Givensrotation, % welche y zu null rotiert if y~=0, cot = x/y; s = 1/sqrt(1+cot^2); c = s*cot; else c=1; s=0; end
Im nachfolgenden Programm werden die Transformationen nicht mehr durch Multiplikation mit vollen Matrizen ausgeführt. Es werden nur noch jene Elemente neu berechnet, die von den Givensrotationen betroffen sind.
Man beachte, dass in MATLAB Vektoroperationen sehr gut dargestellt werden können, z. B. wird durch
rs(i,i-1:n) = -si*rs(i-1,i-1:n) + co*rs(i,i-1:n);
die
A= round(10*rand(7,4)) u=rand(7,1) v=[1 2 3 4]' [m n] = size(A); [Q R] = qr(A); QS =Q; RS = R; % w = Q'*u % anullieren w(n+2:m) und aendern nur Q for i=m:-1:n+2, [si , co]= giv(w(i-1), w(i)); w(i-1) = co*w(i-1) + si*w(i); % QS = QS*G'; h = QS(:,i-1); QS(:,i-1) = co*h + si*QS(:,i); QS(:,i) = -si*h + co*QS(:,i) end % annullieren w(2:n+1) und aendern R und Q for i= n+1:-1:2, [si , co]= giv(w(i-1), w(i)); % w = G*w w(i-1) = co*w(i-1) + si*w(i); % RS = G*RS h = co*RS(i-1,i-1:n) + si*RS(i,i-1:n); RS(i,i-1:n) = -si*RS(i-1,i-1:n) + co*RS(i,i-1:n); RS(i-1,i-1:n) = h % QS = QS*G'; h = QS(:,i-1); QS(:,i-1) = co*h + si*QS(:,i); QS(:,i) = -si*h + co*QS(:,i) end % Addieren jetzt die Rang 1 Mod. zur eRSten Zeile von R RS(1,:) = RS(1,:) + w(1)*v' % RS ist nun Hessenberg und wird reduziert for i = 1:n, [si , co]= giv(RS(i,i), RS(i+1,i)) % RS = G*RS h = co*RS(i,i:n) + si*RS(i+1,i:n); RS(i+1,i:n) = -si*RS(i,i:n) + co*RS(i+1,i:n); RS(i,i:n) = h % QS = QS*G'; h = QS(:,i); QS(:,i) = co*h + si*QS(:,i+1); QS(:,i+1) = -si*h + co*QS(:,i+1) end % Kontrolle AS = A + u*v'; [qs rs] = qr(AS); qs QS rs RS
Peter Arbenz 2008-09-24