
When a routine calls itself either directly or indirectly, it is said to be making a recursive call. Recursion is the third technique for repeatedly executing a command sequence. It, however, does not require any additional built-in Darwin commands. The basic idea behind solving problems via recursion is to break the instance of the problem into smaller and smaller pieces until the pieces are so small they can be solved trivially. We can view a recursive routine as consisting of two parts.
A necessary condition for recursion to work correctly is that progress must always be made at each invocation of the routine. If no progress is made, then the recursion will continue to dive infinitely deeper (and you will eventually run out of memory).
It is required by law that every programming language manual
use the factorial function in an example. We give ours here. Recall
the definition of the factorial of a positive integer:

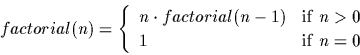
> factorial := proc ( n ) > if (n=0) then > return(1); > else > return(n * factorial(n-1)); > fi; > end: > > factorial(0); 1 > factorial(1); 1 > factorial(5); 120 > factorial(100); 9.3326215443944102e+157
Attempting to pass too large an integer to factorial may produce a rather extreme reaction from Darwin and the operating system you are working with. This is because the depth of recursion (the number of recursive calls) becomes so large, the system runs out of memory.6.1
Recursion is especially convenient for working with phylogenetic
trees. Although there are many different variants of
phylogenetic trees, the basic idea behind all of them is to represent the
ancestral relationships between a set of taxa.
We take this opportunity to introduce the Darwin data types Tree
and Leaf as we will be working with them extensively in
Chapter ![[*]](cross_ref_motif.gif) - Phylogenetic Trees of Part
- Phylogenetic Trees of Part ![[*]](cross_ref_motif.gif) .
We can represent a phylogenetic tree for a set of species as a complete
binary tree6.2 with
the vertices of the tree (the points or nodes) representing
species and the edges (lines that connect points) representing
ancestral relationships.
.
We can represent a phylogenetic tree for a set of species as a complete
binary tree6.2 with
the vertices of the tree (the points or nodes) representing
species and the edges (lines that connect points) representing
ancestral relationships.
There are two types of vertices:
These trees capture the biologic notion of speciation events. In
Figure ![[*]](cross_ref_motif.gif) , a speciation event occured in the
ancestor of all fish (represented by the Swordfish X. Helleri) and
the ancestor of amphibians and mammals.
Next, a speciation occurred in the ancestor of the
amphibians (represented by the frog here) and the ancestor of mammals
and the chicken. Then comes the speciation between the ancestor of
mammals and chicken, followed by a speciation of humans and the
ancestor of mice and rats and, lastly, the divergence of mice and
rats.
, a speciation event occured in the
ancestor of all fish (represented by the Swordfish X. Helleri) and
the ancestor of amphibians and mammals.
Next, a speciation occurred in the ancestor of the
amphibians (represented by the frog here) and the ancestor of mammals
and the chicken. Then comes the speciation between the ancestor of
mammals and chicken, followed by a speciation of humans and the
ancestor of mice and rats and, lastly, the divergence of mice and
rats.
In Darwin we can define tree structures using the types Tree
and Leaf. A Tree structure consists of a left
child, a label and a right child. The left and right children consist of
either another Tree structure or a Leaf structure.
A Leaf structure contains only a label.
The following code creates a Darwin tree for the tree shown in
Figure ![[*]](cross_ref_motif.gif) .
.
> l_l_l_l := Tree( Leaf( 'SH30' ), 'A', Leaf( 'SH29' ) ): > l_l_l := Tree( l_l_l_l, 'B', Leaf( 'SH36' ) ): > l_l := Tree( l_l_l, 'C', Leaf( 'SH20' ) ): > l := Tree( l_l, 'D', Leaf( 'SH23' ) ): > root := Tree( l, 'root' , Leaf( 'SH14' ) ):
This code can be found in file Samples/tree or from the COMPUTATIONAL BIOCHEMISTRY RESEARCH GROUP web site [5]. This tree is a phylogenetic tree formed in Darwin for a set of sequences containing the SH2 domain. We will be using the SH1, SH2 and SH3 domains repeatedly throughout the latter chapters of this book. The following list (also contained in Samples/tree) maps labels for the sequences to the name of the organism from which they came.
> SH2toOrganism := [['SH20', 'CHICKEN'], ['SH30', 'MOUSE'], > ['SH36', 'HUMAN'], ['SH29', 'RAT'], ['SH14','SWORDFISH'], > ['SH23','FROG']]:Let us first design a recursive procedure to print out the tree in a more readable format.
FindOrganism:= proc(label : string)
global SH2toOrganism;
for i from 1 to length(SH2toOrganism) do
current := SH2toOrganism[i];
if (current[1]=label) then
return(current[2]);
fi;
od;
return('Species not know');
end;
PrintTree := proc (T : {Leaf, Tree} )
# The basis case: T is a leaf
if (type(T, Leaf)) then # print out the organism name
printf('%s', FindOrganism(T[1])); # corresponding to the label
else
printf(' [ '); # The recursive case: T is a
PrintTree(T['Left']); # tree with a left and right
printf(' '); # child. Recurse on both.
PrintTree(T['Right']);
printf(' ] ');
fi;
end;
[ [ [ [ [ MOUSE RAT ] HUMAN ] CHICKEN ] FROG ] SWORDFISH ]
The recursive case in PrintTree occurs when T is a Tree structure. Since phylogenetic trees are complete binary trees, T must have both a left and right subtree. We call PrintTree with the left subtree as a parameter and then we call PrintTree with the right subtree as a parameter. The basis case in our recursive procedure PrintTree occurs when the parameter T consists of only a Leaf structure. In this case it passes the label of the Leaf to the FindOrganism function. This function matches the Leaf label to the corresponding organism name found in SH2toOrganism and returns it to PrintTree.
We will see many more examples of recursion with Darwin trees in later chapters. It can be difficult to follow (never mind write) a recursive routine at first but the effort is worthwhile. What may take many lines of code to do iteratively, may take only a few lines recursively. In this way, recursion can offer a crisp elegant perspective of many routines.