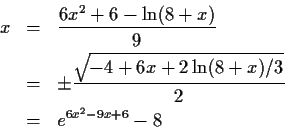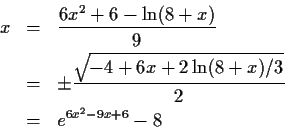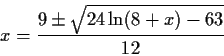

Next: Substitute all non-polynomials.
Up: Building additional iterators
Previous: Building additional iterators
One of the ways in which we can create new, and hopefully better,
iterators is by isolating subexpressions which are
easy to invert, instead of isolating x.
For example, the equation
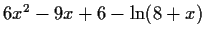 generates the iterators
generates the iterators
For the initial value x0=1.23, all these iterators fail.
The first one and the third one grow without bound,
the positive second iterator converges too slowly and the
negative oscillates between one value and its conjugate.
For this equation we could instead isolate the polynomial part
solve it treating the 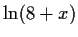 as a constant,
and obtain two new iterators.
as a constant,
and obtain two new iterators.
Notice that these new iterators have only one occurrence of x on
the rhs, compared to two for the previous ones.
The positive choice for this iterator is successful
and converges very quickly to
x=0.7595...+0.2753...i.
This is not a general rule, we could certainly find examples which
show the contrary, but in general it is expected that such
groupings will produce better iterators as they capture more information
about the inverse.
So we will use the following rule, for each iterator F(x) which
is a sum of a polynomial part and a non polynomial part, i.e.
x = F(x) = G(x) + p(x)
we will produce an iterator which is
x-p(x)=G(x) and each
iteration consists of evaluating
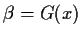 and then solving the
polynomial
and then solving the
polynomial
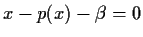 .
Removing the polynomial part will decrease
the number of occurrences of x on the rhs, and hence improve
our measure of quality of the iterators.
The iterator can be written using Maple's
RootOf2
notation as
.
Removing the polynomial part will decrease
the number of occurrences of x on the rhs, and hence improve
our measure of quality of the iterators.
The iterator can be written using Maple's
RootOf2
notation as
A polynomial iterator, with degree d on its lhs, will normally
have d roots.
This has a cardinality advantage over handling a polynomial
iterator by its individual terms.
If the individual terms of the polynomial are isolated one by one,
and for each monomial xk, k roots have to be
considered, up to d(d+1)/2 iterators could be generated.
The drawback is obvious, instead of having a closed form solution
for the iterator, we have to solve a polynomial of degree d, and
this is typically an iterative process for d>2.
Selecting which root of the polynomial to use is non trivial.
When roots are given by a formula, e.g. for d=2, then it is easy
to write two iterators, one for each root.
But when the roots are found numerically, it is not possible
to have a consistent way of using the same root on successive iterations.
Actually, the term ``same root'' does not even make sense for
different polynomials, it only makes sense when the roots
can be expressed as functions of the coefficients.
On the other hand, if the polynomial iterator is converging,
we want to select the root which is closest to the iteration value.
I.e.
and we select the root which is closest to xi.
Since this selection is necessary for convergence, we will use it
in every step of the algorithm.
Furthermore, many iterative methods for solving polynomials can
profit significantly from starting their iterators at an
approximation of the root; the correct root could come almost for free.
For example, for the solution of the equation
we define the iterator
If we start with x0 = 1, then the rounded roots of the polynomial are
The root which is closest to x0=1 is
0.758845...Hence we set
x1=0.758845....
For the second iteration the polynomial to solve, is
z5 -6z4 +5z3 +6z -5 =-1.11236...The roots of this polynomial are
and the root closest to x1 is
0.586566... which
becomes x2.
This process converges quite quickly,
x3=0.561733...,
x4=0.563302...,
x5=0.563168..., etc.
This root selection can also be treated as a multiple value function
problem, which is discussed in the next section.
Table 2:
Iterators which have a non-linear polynomial in their lhs
| 66644 random equations producing 59428 iterators |
| method |
failures |
| converged to a root |
44.64% |
converged to a non-root |
1.67% |
| failed |
55.36% |
diverged |
21.22% |
| average time |
1.593 |
outside domain |
18.06% |
| time per root |
3.569 |
too many iterations |
4.79% |
| |
|
iterator fails |
0.00% |
| iterators per equation |
.892 |
no iterators |
54.26% |
|
Table 2 shows the simulation results for polynomial
lhs iterators.
Almost 45% of the iterators yield a root, in time which is of the
same order of magnitude as for the simple iterators.


Next: Substitute all non-polynomials.
Up: Building additional iterators
Previous: Building additional iterators
Gaston Gonnet
1998-07-08