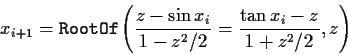| 66644 random equations producing 14398 iterators |
| method |
failures |
| converged to a root |
11.64% |
converged to a non-root |
.39% |
| failed |
88.36% |
diverged |
6.22% |
| average time |
.672 |
outside domain |
3.51% |
| time per root |
5.768 |
too many iterations |
1.15% |
| |
|
iterator fails |
0.00% |
| iterators per equation |
.216 |
no iterators |
88.73% |
|