Building additional iterators

It is easy to see that we can create an infinite number of iterators. For instance, for any iterator x = F(x), and arbitrary a,

$$x = \frac{ F(x)+ax}{a+1}$$

will also be fixed point iterator giving the same solution set for any $a \neq -1$.

A natural question to ask is, which iterator is better? This question is nontrivial to answer, and contradicts the spirit of the heuristic, which is to try all of them. We would like to try a large number of formulas and not conjecture which is the best one and use it alone. Yet an intuitive and very economic measure of the quality of the iterators is $\char93 _x(F(x))$, the number of occurrences of xon the right-hand side of the iterator. A smaller $\char93 _x(F)$ is considered better. The degenerate case is a good example. If $\char93 _x(F) = 0$, we have an explicit expression for the root. Using iterators which have the minimal $\char93 _x(F)$ guarantees, to a certain degree, that we will not be generating more complicated trivial iterators.

If at any point during our isolation or after trial simplification, the resulting equation has a smaller number of occurrences of x, we will derive all possible iterators arising from this shortened equation. For example,

$$\begin{eqnarray*}x \ln x & = & x^{1.001}\\ \ln x & = & \frac{x^{1.001}}{x} \\ \ln x & = & x^{0.001} \\ \end{eqnarray*}$$

The grouping of powers caused a simplification and from this equation we obtain two iterators

$$\begin{eqnarray*}x & = & e^{x^{0.001}} \\ x & = & ( \ln x )^{1000} \\ \end{eqnarray*}$$

The first one was obtained before but the second one is new and in this case it is useful to find the largest of the roots of the original equation.

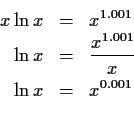
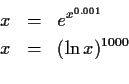
The use of $\char93 _x(F)$ as a measure of iterator quality seems to work in practice, although we cannot prove this generally. Certainly there are examples of two iterators for the same equation, where $\char93 _x(F_1)<\char93 _x(F_2)$, and F₁ behaves worse than F₂.