Transcendental Iterators.

The technique of explicitly finding roots of polynomials can be extended to cases involving transcendental functions with multivalued inverse functions.

Consider the equation $\sin x = x/100$. Providing for all solutions of $\sin x$ yields three iterators:

$$\begin{eqnarray*}x & = & 100\sin x \\ x & = & \sin^{-1}(x/100)+2\pi n \\ x & = & \pi - \sin^{-1}(x/100)+2\pi n \\ \end{eqnarray*}$$

where n iterates over all of the integers and the $\arcsin$ returns the principal branch. The first iterator diverges chaotically. The other two, however, either converge to solutions or else fail due to the $\arcsin$ evaluating to a complex number ( |x/100| > 1).

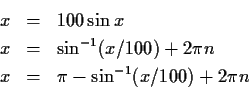
Furthermore, all solutions can be generated by simply using different values of n. For the first equation, values $-15 \le n \le 15$ will yield the even numbered roots, whereas values $-16 \le n \le 15$ will yield the remaining roots when used in the second equation. Other values of n diverge. (The asymmetry comes from the positive sign on the first $\pi$; the iterator $x = -\pi - \sin^{-1}(x/100)+2\pi n$would supply the same set of roots with $-15 \le n \le 16$). The solution obtained is unrelated to the initial guess used; almost any starting value acceptable to the $\arcsin$ converges to the same root for a given choice of iterator and n.