

Next: Building additional iterators
Up: Partial inverse heuristic for
Previous: Evaluation by simulation.
The question of convergence of the different iterators can be
partially answered.
For functions with two occurrences of the unknown, 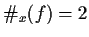 ,
in general either one or the other derived iterator converges.
This is proven as follows.
,
in general either one or the other derived iterator converges.
This is proven as follows.
Let
f(x1,x2)=0 be the equation to be solved, identifying
each occurrence of x by x1 and x2.
Let Fi(x) be the iterator derived from inverting f on xi.
Formally this means that
f(F1(x),x) = 0
and
f( x, F2(x) ) = 0
Let 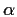 be a root of f,
be a root of f,
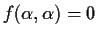 .
The convergence of the iterators depends on
.
The convergence of the iterators depends on
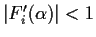 .
By computing derivatives with respect to x of the above
identities, we find
.
By computing derivatives with respect to x of the above
identities, we find
For this system of equations to have a non-null solution in
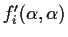 ,
its determinant must be zero, or
,
its determinant must be zero, or
and from this
So unless both absolute values are equal to one, then one
iterator converges while the other diverges.
This is a very encouraging result, it guarantees that one of the
iterators will succeed for each of the roots.
For
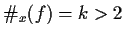 the results are much weaker.
For general x, the condition becomes
the results are much weaker.
For general x, the condition becomes
Then, if k-1 of the values
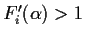 ,
the
remaining one must be between 0 and 1 and hence the corresponding
iterator converges.
This does not guarantee convergence for every case, as all
,
the
remaining one must be between 0 and 1 and hence the corresponding
iterator converges.
This does not guarantee convergence for every case, as all
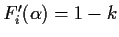 ,
i.e.
,
i.e.
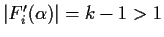 is also a possible solution and in this case all iterators
will diverge.
is also a possible solution and in this case all iterators
will diverge.
The above theorem for two occurrences, strongly
suggests that grouping variables (if possible) while
building the iterators, is a good strategy.


Next: Building additional iterators
Up: Partial inverse heuristic for
Previous: Evaluation by simulation.
Gaston Gonnet
1998-07-08
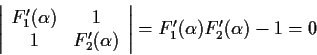
![]() the results are much weaker.
For general x, the condition becomes
the results are much weaker.
For general x, the condition becomes
