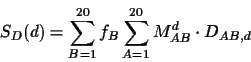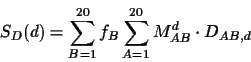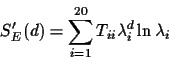Next: Scores are inconsistent to
Up: Dayhoff Scores and Evolutionary
Previous: Dayhoff Scores and Evolutionary
Naturally we would assume that a lower PAM distance corresponds to
a higher score, i.e. a higher probability that the sequences are
related. First we show that this assumption is true when the
lengths of the sequences are the same. To verify if smaller PAM
distances correspond to larger scores, we have to look at the
expected value of the score SD(d) as a function of the PAM
distance d. To do this we look at sequences with length n. The
expected score SD(d) for each aligned amino acid is
where DAB,d is the score of amino acids A and B at
PAM distance d and the probabilities are from equation 1.
In our case, Dd is a Dayhoff matrix for PAM distance d.
If we want the expected score for the whole
sequences, we have to multiply this value by n. Calculating
SD(d) for each d from 0 to 200, we get the plot in Figure
2.
Figure 2:
The expected score S(d) as a
function of the PAM distance d.
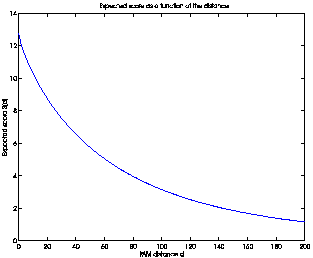 |
The function is monotonic and decreasing, meaning that a
larger PAM distance d does correspond to a lower score SD(d).
The graph is only a "visual" proof. To prove this, we have to
analyze the derivative of SD(d) with respect to d.
To compute this derivative, Md can be rewritten as
where 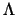 is a diagonal matrix containing the
eigenvalues of M.
In
is a diagonal matrix containing the
eigenvalues of M.
In 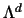 each diagonal element is
each diagonal element is
 .
For any matrix E, SE(d) can be rewritten as
.
For any matrix E, SE(d) can be rewritten as
 |
(2) |
If we multiply everything out we can rewrite SE(d) as
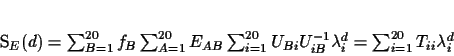 |
(3) |
where Tii is the ith diagonal entry in the matrix
T
= U-1F ET U (F is a diagonal matrix with the frequencies
Fii = fi).
Its derivative is
and can be computed and verified to be negative for all d in
the range 0 to 250, for the Dayhoff matrix in
[9].



Next: Scores are inconsistent to
Up: Dayhoff Scores and Evolutionary
Previous: Dayhoff Scores and Evolutionary
Chantal Korostensky
1999-07-14