


Next: Methods
Up: Introduction
Previous: Scoring Pairwise Sequence Alignments
To calculate the score with the SP measure [Carillo and Lipman, 1988], all
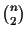 scores of the pairwise alignments within the MSA
(see Definition 2.6) are added up. SP methods are
obviously deficient from an evolutionary perspective
[Altschul and Lipman, 1989]. Consider a tree (Figure 2)
constructed for a family containing five proteins. The score of a
pairwise alignment
scores of the pairwise alignments within the MSA
(see Definition 2.6) are added up. SP methods are
obviously deficient from an evolutionary perspective
[Altschul and Lipman, 1989]. Consider a tree (Figure 2)
constructed for a family containing five proteins. The score of a
pairwise alignment
 evaluates the
probability of evolutionary events
on edges (u, A) and (u, B) of the tree; that is, the edges that represent
the evolutionary distance between sequence A and sequence B.
Likewise, the score of a pairwise alignment
evaluates the
probability of evolutionary events
on edges (u, A) and (u, B) of the tree; that is, the edges that represent
the evolutionary distance between sequence A and sequence B.
Likewise, the score of a pairwise alignment
 evaluates the likelihood of evolutionary events on edges (C, w),
(w, v) and (v, D) of the tree.
evaluates the likelihood of evolutionary events on edges (C, w),
(w, v) and (v, D) of the tree.
Figure 2:
Traversal of a trees using the SP
measure. Some edges are traversed more often than others. The
numbers on the edges represent the number of "ticks".
 |
By adding "ticks" to the evolutionary tree that are drawn each
time an edge is evaluated when calculating the SP score (Figure
2), it is readily seen that with the SP method
different edges of the evolutionary tree of the protein family are
counted a different numbers of times. In the example tree on the
left side that corresponds to the MSA of figure
1, edges (r, u), (r, w) and (w, v) are
each counted six times by the SP method, while edges (u, A),
(u, B), (v, D), (v, E), and (w, C) are each counted four
times. The numbers on the edges are the numbers of "ticks". It
gets worse as the tree grows (see tree on the right). There is no
theoretical justification to suggest that some evolutionary events
are more important than other ones.
Thus, SP methods are intrinsically problematic from an
evolutionarily perspective for scoring MSAs. This was the
motivation to developed a scoring method that evaluates each edge
equally. In addition, we wanted a scoring function that does not
depend on the actual tree structure.
We report here a ``circular sum'' (or CS) method for evaluating
the quality of an MSA. The method uses a solution to the Traveling Salesman Problem, which identifies a
circular tour through an evolutionary tree connecting the
sequences in a protein family. The algorithm gives an upper bound,
the best score that can possibly be achieved by any MSA for a
given set of protein sequences. Both the bound and the circular
tour can be derived without an explicit knowledge of the correct
evolutionary tree; thus the method can be applied without need to
address the mathematical issues involved in tree construction.
Last, it gives us an absolute score of MSAs which is important in
designing and verifying MSA heuristics.
Both the tree construction problem and the Traveling Salesman
Problem are NP complete. But the Traveling Salesman Problem (see
next section) has been studied very extensively
[Johnson, 1990,Johnson, 1987], and optimal solutions can be
calculated within a few hours for up to 1000 cities and in a few
seconds for up to 100 cities, whereas the construction of
evolutionary trees is still a big problem. There are heuristics
for large scale problems that calculate near optimal solutions
that are within 1% to 2% of the optimum
[Padberg and Rinaldi, 1991,Groetschel and Holland, 1991].



Next: Methods
Up: Introduction
Previous: Scoring Pairwise Sequence Alignments
Chantal Korostensky
1999-07-14

