Scoring of MSAs without evolutionary trees

The CS algorithm provides a method to evaluate a specific MSA or to compare different algorithms for constructing MSAs. To do so, we abandon scores obtained pairwise from OPAs. Instead, the pairwise relationship between two sequences in the protein family are extracted from the MSA itself. These are scored using a Dayhoff matrix without dynamic programming re-alignment to give an optimal alignment. These are MSA-derived pairwise alignments (MPA).

Definition 2.5   The function S(x, y) scores two symbols $x, y \in \Sigma'$:
$S(x, y) = \left\{ { \begin{tabular}{l} $DM(x, y)$ , if $x \neq ''\_''$\space ... ... the gap length \\ \cite{Altschul86,BennerIndels93} \end{tabular}} \right.$
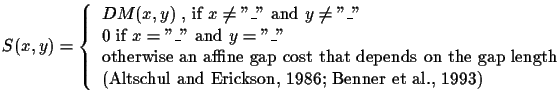
DM is an entry in a Dayhoff matrix [Schwarz and Dayhoff, 1979,Gonnet et al., 1992].

The function S(x, y) (see Definition 2.5) scores two symbols x, y that are either amino acids or gap characters in our case.

Definition 2.6   The induced MSA-derived pairwise alignment MPA(a_i, a_i) of two sequences $a_i, a_j \in \mbox{\rm A}$ is:
$MPA(a_1, a_2) = \sum\limits_{m=1}^{k} S(a_i[m], a_j[m])$

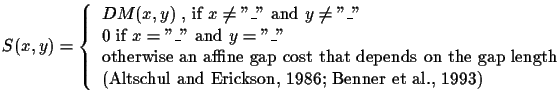
MPA scores must be equal to or less than the scores obtained from the OPA pairwise alignments. The CS method can be applied now again without the need for an explicitly defined evolutionary tree by repeating the procedure outlined above, but using MPA scores instead of OPA scores. The CS score of the MSA is the sum of MPA scores in the circular order C divided by two:

Definition 2.7   The score $CS(\mbox{\rm A})$ of an MSA $\mbox{\rm A}$ is defined as: $CS(\mbox{\rm A}) = \frac{1}{2} \sum\limits_{i=1}^{n} MPA(a_{C_{i}}, a_{C_{i+1}})$ where C_n+1 = C₁.

Note that if there is a deletion in both sequences, there is no penalty (score is zero) because that deletion happened in some ancestor, and its penalty has been counted already ².

Lemma 2.4 (Upper Bound)   Let $\cal{A}$ be the set of all possible MSAs that can be generated for a given set of sequences $S=\{s_1, s_2, .., s_n\}$. The maximal score CS_max(S) serves as an upper bound for the score of any MSA $\mbox{\rm A}$ that can be built from S:
$CS_{max}(S) \geq \max \limits_{\mbox{\rm A}\in \cal{A}} CS(\mbox{\rm A})$

Proof 2.4   OPA scores are optimal. Therefore, CS_max(S), which is the sum of OPA scores in circular order obtained by a TSP algorithm, is also maximal. Assume this last statement is wrong there exists another score $CS'(\mbox{\rm A})$ that is higher than CS_max(S). Since that score $CS'(\mbox{\rm A})$ is a sum of MPA scores, it would follow that at least one of the MPA scores is higher than the corresponding OPA score, which is a contradiction.

Whenever we score an MSA, regardless of the algorithm used to generate it, the score of this alignment must be less than or equal to the upper bound CS_max(S). Hence the upper bound can be used to evaluate a given MSA. The closer the score of a calculated MSA is to the upper bound, the better the MSA is.
Note that in many cases, as in the following example and always when none of the optimal pairwise alignments of S have gaps, then the score of the MSA $CS(\mbox{\rm A}) = CS_{max}(S)$.
Example 2.2:  The table to the right in Figure 9 shows the pairwise MPA scores of the sequences from the MSA on the left. It is easy to verify that the longest tour is (A, B, C, D, E, A) and that it is a circular tour in the corresponding tree (see Figure 1). The score of the MSA is the sum of pairwise alignments in circular order divided by two, so $F(\mbox{\rm A}) = (336 + 79 + 171 + 327 + 110) /2 = 512$. Here the MSA has the optimal score CS_max(S)..

  

Figure 9: An MSA and a table containing the pairwise scores

A: RPCVCP___VLRQAAQ__QVLQRQIIQGPQQLRRLF_AA
B: RPCACP___VLRQVVQ__QALQRQIIQGPQQLRRLF_AA
C: KPCLCPKQAAVKQAAH__QQLYQGQLQGPKQVRRAFRLL
D: KPCVCPRQLVLRQAAHLAQQLYQGQ____RQVRRAF_VA
E: KPCVCPRQLVLRQAAH__QQLYQGQ____RQVRRLF_AA

	A	B	C	D	E
A	0	336	27	44	110
B	336	0	79	56	99
C	27	79	0	171	176
D	44	56	171	0	327
E	110	99	176	327	0