Probability of an evolutionary tree configuration

To obtain the probability for an entire evolutionary tree configuration, one must sum the logarithms of the probabilities of each event represented by the tree. For the example tree in Figure 10, the total evolutionary history has six associated probabilities: A $\rightarrow$B, A $\rightarrow$C, B $\rightarrow$1, B $\rightarrow$2, C $\rightarrow$3 and C $\rightarrow$4.

  

Figure 10: A sample evolutionary tree

If we knew the sequences of the ancestral proteins at the internal nodes of the tree, the probability of the entire tree is:

$$% latex2html id marker 352 Pr\{ \mbox{tree of Figure \ref{fig... ...box{ C$\rightarrow$ 3 } \} Pr\{ \mbox{ C$\rightarrow$ 4 } \}$$ (4)

where $Pr\{ \mbox{ X$\rightarrow$ Y } \}$ is interpreted as the probability of mutating from the amino acid in the node X to the amino acid in node Y according to the distance of the edge X-Y. The individual probabilities would be obtained by aligning the protein sequences at the beginning and end of each episode of evolution and scoring them using a Dayhoff matrix (for example) as described above. Normally, of course, the sequences for the ancestor proteins A, B and C are not known, as the organisms that contained them have long since died. In [Gonnet and Benner, 1996], a formula for the probability of an entire evolutionary configuration (the ensemble of the phylogenetic tree and the corresponding MSA) is derived. It corresponds exactly to the notion of computing the probability of traversing each edge of the tree. We can compute the probability of the tree configuration by adding the probabilities of all episodes represented by each of the edges.
Hence a tree scoring function F(T) must score each edge of the tree exactly once. Let T(A) be the tree for the MSA $\mbox{\rm A}$. The function $CS(\mbox{\rm A})$ approximates the probability of T, as every edge is evaluated equally ³.

Lemma 2.5 (Maximum Score)   The maximal score CS_max(S) is both an upper bound on the score for the tree and it is also an upper bound on the score of an MSA for the underlying sequences.

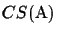
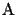
Proof 2.5   We have already shown that CS_max(S) is the upper bound for $CS(\mbox{\rm A})$ for any $\mbox{\rm A}$ derived from S. Since the formula for deriving the score is exactly the same for both trees and MSAs, CS_max(S) also serves as an upper bound for the score of any tree T(S) that can be derived from S. Therefore, there can be no tree and also no MSA with a higher score than CS_max(S) for a given set of sequences S.

We have now a way to determine a circular order and thus an upper bound on the score of an MSA and its associated evolutionary tree for a set of sequences. This score has been obtained without requiring the calculation of an evolutionary tree. Only the sequences at the leaves and their OPA/MPA scores with each other are needed.