Improving Alignments With Gap Blocks

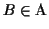
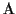
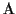
Definition 3.5   The score S(B) of a block $B \in \mbox{\rm A}$ is the maximum possible score of the MSA $\mbox{\rm A}$ that can be obtained by shifting the gaps in $\mbox{\rm A}$ that correspond to the gaps within the block B.

Once we have all the gap blocks we can optimize the MSA $\mbox{\rm A}$ by shifting the gaps in each B that correspond to the real gaps in the alignment $\mbox{\rm A}$. The problem is that some gap blocks may overlap, that is two different gap blocks Bⁱ and B^j may share the same gaps. Of course, only either Bⁱ or B^j can be chosen in the final alignment. Whenever this happens, we want to select the block with the best score. For any two blocks Bⁱ, B^j in P, if the block Bⁱ overlaps with some other block B^j, score both according to Definition and remove the block with the lower score from P. For each block B in P, shift and combine the gaps in the MSA $\mbox{\rm A}$ that correspond to the block Bⁱ and keep the change if the score increases.
Example 3.2:  After applying the above procedures to the MSA in Figure , we end up with an MSA that has a much better score and only has 4 indel events. In addition, we can use the gaps of the MSA to construct the corresponding evolutionary tree (see Section 4).

Score of the alignment: 2400.081
Maximum possible score: 2472.632

a1	PDCVCPTLKQAAKAVRLQG___________QHQPMQVRKIYQTAKHLPNVC
a2	PVCVCPTLRQAARAVSLQG___________QHGPFQSRKIYKTAKYLPNIC
a3	PVCVCPTLKQAARAVSLQG___________QHGPFQSRKIYQSAKYLPNIC
a4	QVCVCPTLKQAAKSVRVQG___________QHGPFQSTRIYQIAKNLPNVC
a5	PLCVCPTLKGASKAVKQQVRQQLEQQG___QQGPHVISRIYQTATHLPKVC
a6	PLCVCPTLKGASKAVKQQVRQQQGQQG___QQLQQVISRIYQTATHLPKVC
a7	PLCVCPTLKGASKAVRQQVRQQQGQQM_QGQQMQQVISRVYQTATHLPRVC
a8	PLCVCPTLKGASKAVKQQIRQQGQQQGQQGQQLQHEISRIYQTATHLPRVC
a9	PLCVCPTLKGAAKAVKQQIQQQGQQHGQQGQQLQHEIRRIYQTATHLPKVC
a10	PLCVCPTLKGASKAVKQQIQQQGQQQG_____KLQMVSRIYQTATHLPKVC
a12	PLCVCPTLKGASKAVKQQIQQQGQQQG_____KQQMVSRIYQTATHLPKVC
a13	PLCVCPTLRGASKAVKQQIQQQEQQQG_____KQQMVNRIYQTATHLPKVC