We present a new tree construction method that constructs a tree
with minimum score for a given set of sequences. To do this,
the problem of tree construction is reduced to the Traveling
Salesman Problem (TSP). The input for the TSP algorithm are the
pairwise distances of the sequences and the output is a circular tour
through the optimal, unknown tree plus the minimum score of the
tree. The circular order and the score of the optimal tree can be
used to construct the topology of the tree in
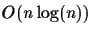
time
where
n is the number of input sequences. We can guarantee that
we reconstruct a correct evolutionary tree if the error for each
distance measurement is smaller than
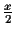
,
where
x is
the shortest edge in the tree. For data sets with large errors, a
dynamic programming approach is used to reconstruct the tree.
Keywords: tree construction, Traveling Salesman, circular order, evolution